Randomized branch sampling
(→Randomized branch sampling) |
|||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Ficontent}} |
| − | + | ||
| − | + | ||
| − | + | ||
Total tree bark volume is a variable that cannot easily be directly measured. The “true” volume could theoretically be determined by stripping off all bark and using water displacement to measure volume. However, this is impractical and the obvious way to go is to develop simple models based on pragmatic sampling techniques. | Total tree bark volume is a variable that cannot easily be directly measured. The “true” volume could theoretically be determined by stripping off all bark and using water displacement to measure volume. However, this is impractical and the obvious way to go is to develop simple models based on pragmatic sampling techniques. | ||
| − | |||
To sample variables such as bark we imagine the tree as a population of above ground N stem and branch sections where each section goes from one fork (or node) to the next – except for the bottom and top sections at which the tree begins and ends, respectively. From this set of N sections we would then select n sections as sample. | To sample variables such as bark we imagine the tree as a population of above ground N stem and branch sections where each section goes from one fork (or node) to the next – except for the bottom and top sections at which the tree begins and ends, respectively. From this set of N sections we would then select n sections as sample. | ||
| − | |||
Doing so by [[simple random sampling]] (SRS), for example, we could directly estimate the mean bark volume per section. However, for estimation of the total, we would then face the problem that we needed to know the [[population]] size, i.e. the total number of sections to determine the expansion factor to extrapolate the mean section estimate to the whole tree. If the population size is known, we also know the [[inclusion probability]] for each section ‑ 1/N for simple random sampling ‑: this probability is required to develop an unbiased estimator for any design based sampling strategy. This is what we call [[probabilistic sampling]]. | Doing so by [[simple random sampling]] (SRS), for example, we could directly estimate the mean bark volume per section. However, for estimation of the total, we would then face the problem that we needed to know the [[population]] size, i.e. the total number of sections to determine the expansion factor to extrapolate the mean section estimate to the whole tree. If the population size is known, we also know the [[inclusion probability]] for each section ‑ 1/N for simple random sampling ‑: this probability is required to develop an unbiased estimator for any design based sampling strategy. This is what we call [[probabilistic sampling]]. | ||
| − | |||
In addition, to be able to carry out simple [[random selection]], we also need to define the [[population|sampling frame]] so that we can unambiguously identify individual sampling elements sections, in our case). Both tasks (finding the population size and then defining the sampling frame), are clearly impractical for estimating total tree bark utilizing a simple random sampling approach. | In addition, to be able to carry out simple [[random selection]], we also need to define the [[population|sampling frame]] so that we can unambiguously identify individual sampling elements sections, in our case). Both tasks (finding the population size and then defining the sampling frame), are clearly impractical for estimating total tree bark utilizing a simple random sampling approach. | ||
| − | |||
Randomized branch sampling (RBS) is a sampling strategy that facilitates the drawing of a probabilistic sample without ''a priori'' defining the sampling frame. The inclusion probabilities of the selected population elements are determined in the course of the sampling process itself. RBS was developed by Jessen (1955)<ref>Jessen R.J. 1955. Determining the fruit count on a tree by randomized branch sampling. Biometrics 11:99-109</ref> for estimation of fruit count in orchards and has since been successfully applied to estimation of various tree variables (e.g. Valentine ''et al.'' 1984<ref> Valentine TV, LM Tritton and GM Furnival. 1984. Subsampling Trees for Biomass, Volume or Mineral Content. Forest Science 30(3):673-681</ref>, Gregoire ''et al.'' 1995<ref>Gregoire TG, HT Valentine and GM Furnival. 1995. Sampling methods to estimate foliage and other characteristics of individual trees. Ecology 76:1181-1194</ref>, Good ''et al.'' 2001<ref name="Good 2001">Good NM, M Paterson, C Brack and .K Mengersen. 2001. Estimating Tree Component Biomass Using Variable Probability Sampling Methods. Journal of Agricultural, Biological, and Environmental Statistics 6(2):258–267</ref>, Cancino 2003, Cancino and Saborowski 2005<ref>Cancino J and J Saborowski. 2005. Comparison of randomized branch sampling with and without replacement at the first stage. Silva Fennica 39(2):201-216.</ref>). | Randomized branch sampling (RBS) is a sampling strategy that facilitates the drawing of a probabilistic sample without ''a priori'' defining the sampling frame. The inclusion probabilities of the selected population elements are determined in the course of the sampling process itself. RBS was developed by Jessen (1955)<ref>Jessen R.J. 1955. Determining the fruit count on a tree by randomized branch sampling. Biometrics 11:99-109</ref> for estimation of fruit count in orchards and has since been successfully applied to estimation of various tree variables (e.g. Valentine ''et al.'' 1984<ref> Valentine TV, LM Tritton and GM Furnival. 1984. Subsampling Trees for Biomass, Volume or Mineral Content. Forest Science 30(3):673-681</ref>, Gregoire ''et al.'' 1995<ref>Gregoire TG, HT Valentine and GM Furnival. 1995. Sampling methods to estimate foliage and other characteristics of individual trees. Ecology 76:1181-1194</ref>, Good ''et al.'' 2001<ref name="Good 2001">Good NM, M Paterson, C Brack and .K Mengersen. 2001. Estimating Tree Component Biomass Using Variable Probability Sampling Methods. Journal of Agricultural, Biological, and Environmental Statistics 6(2):258–267</ref>, Cancino 2003, Cancino and Saborowski 2005<ref>Cancino J and J Saborowski. 2005. Comparison of randomized branch sampling with and without replacement at the first stage. Silva Fennica 39(2):201-216.</ref>). | ||
| − | |||
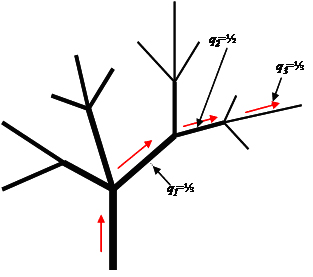
The principle of RBS can be visualized as a randomized unidirectional walk on a path along the network of stem sections starting from the bottom of the tree or another defined starting point to a defined end point (in our case up to a minimum branch diameter of 5 cm). Going along the path, at each fork a probability-based decision (utilizing random number tables or dice) is made to select the branch along which to proceed. Therefore, for each fork, the inclusion probability qi for the next section i is known. This permits the calculation of the overall selection probability for each section within the path as the product of the inclusion probabilities of all preceding sections. In Figure 3, for illustration, the marked outmost section has selection probability <math>p_3 = q_1 * q_2 * q_3</math>. In that case, the first section (the stem) has an inclusion probability <math>q_0 =1</math> and therefore also <math>p_0 = 1</math> because that section is part of all possible sample paths. | The principle of RBS can be visualized as a randomized unidirectional walk on a path along the network of stem sections starting from the bottom of the tree or another defined starting point to a defined end point (in our case up to a minimum branch diameter of 5 cm). Going along the path, at each fork a probability-based decision (utilizing random number tables or dice) is made to select the branch along which to proceed. Therefore, for each fork, the inclusion probability qi for the next section i is known. This permits the calculation of the overall selection probability for each section within the path as the product of the inclusion probabilities of all preceding sections. In Figure 3, for illustration, the marked outmost section has selection probability <math>p_3 = q_1 * q_2 * q_3</math>. In that case, the first section (the stem) has an inclusion probability <math>q_0 =1</math> and therefore also <math>p_0 = 1</math> because that section is part of all possible sample paths. | ||
| Line 23: | Line 15: | ||
[[image:SkriptFig_102.jpg|center|thumb|1000px|'''Figure 3.''' Illustration of randomized branch sampling. The path selected here follows the arrows along the branches. For each section its specific inclusion probability is determined by the random selection carried out at its starting point. The overall selection probability is then calculated as the product of the specific selection probabilities of all preceding sections. The first section (stem) is always “selected”, so that q<sub>0</sub>=1.]] | [[image:SkriptFig_102.jpg|center|thumb|1000px|'''Figure 3.''' Illustration of randomized branch sampling. The path selected here follows the arrows along the branches. For each section its specific inclusion probability is determined by the random selection carried out at its starting point. The overall selection probability is then calculated as the product of the specific selection probabilities of all preceding sections. The first section (stem) is always “selected”, so that q<sub>0</sub>=1.]] | ||
| − | |||
| − | |||
Knowing the inclusion probability for each section of a path, an estimator for the total of the target variable can be developed using the Hansen-Hurwitz estimator. The total <math>\tau</math> can then be estimated from one path of ''m'' sections <math>y_i</math> selected with probabilities <math>p_i</math> by | Knowing the inclusion probability for each section of a path, an estimator for the total of the target variable can be developed using the Hansen-Hurwitz estimator. The total <math>\tau</math> can then be estimated from one path of ''m'' sections <math>y_i</math> selected with probabilities <math>p_i</math> by | ||
| − | + | :<math> \hat \tau = \frac {1}{m} \sum_{i=1}^m \frac {y_i}{p_i}</math> | |
| − | :<math> \hat \tau = \frac {1}{m} \sum_{i=1}^m \frac {y_i}{p_i}</math> | + | |
| − | + | ||
<div style = "float:right; margin-left:4em"> | <div style = "float:right; margin-left:4em"> | ||
| Line 37: | Line 25: | ||
|} | |} | ||
</div> | </div> | ||
| − | |||
Following statistical sampling principles one path provides one [[independent observation]]. This observation is composed of several “sub‑observations”, the sections. This is the same principle which is also applied in [[Bitterlich sampling]], where from one sample point various sample trees are included with probability proportional to their [[basal area]]; the sample tree values are then combined to one sample point observation by weighting them according to their individual inclusion probabilities. For randomized branch sampling the estimation mechanism is illustrated in Figure 4: dividing the observed section value by its per-section selection probability provides an estimation of the total on this section level (Good et al. 2001<ref name="Good 2001" />). | Following statistical sampling principles one path provides one [[independent observation]]. This observation is composed of several “sub‑observations”, the sections. This is the same principle which is also applied in [[Bitterlich sampling]], where from one sample point various sample trees are included with probability proportional to their [[basal area]]; the sample tree values are then combined to one sample point observation by weighting them according to their individual inclusion probabilities. For randomized branch sampling the estimation mechanism is illustrated in Figure 4: dividing the observed section value by its per-section selection probability provides an estimation of the total on this section level (Good et al. 2001<ref name="Good 2001" />). | ||
| − | |||
If one path constitutes a sample of size ''n = 1'', then more paths need to be selected per tree if estimation of precision is an issue. From ''n'' selected paths we generate ''n'' bark volume estimations <math> \hat V_j</math> the mean of which is taken as best estimate | If one path constitutes a sample of size ''n = 1'', then more paths need to be selected per tree if estimation of precision is an issue. From ''n'' selected paths we generate ''n'' bark volume estimations <math> \hat V_j</math> the mean of which is taken as best estimate | ||
| − | |||
:<math>\bar V = \frac {1}{n} \sum_{j=1}^n \hat V_j </math> | :<math>\bar V = \frac {1}{n} \sum_{j=1}^n \hat V_j </math> | ||
| − | |||
with estimated variance | with estimated variance | ||
| − | + | :<math>v\hat ar (\bar V) = \frac {s^2}{n} = \frac {1}{n} \frac {\sum_{j=1}^n (\hat V_j - \bar V)^2}{(n-1)}</math> | |
| − | :<math>v\hat ar (\bar V) = \frac {s^2}{n} = \frac {1}{n} \frac {\sum_{j=1}^n (\hat V_j - \bar V)^2}{(n-1)}</math> | + | |
==References== | ==References== | ||
Latest revision as of 13:30, 26 October 2013
Total tree bark volume is a variable that cannot easily be directly measured. The “true” volume could theoretically be determined by stripping off all bark and using water displacement to measure volume. However, this is impractical and the obvious way to go is to develop simple models based on pragmatic sampling techniques.
To sample variables such as bark we imagine the tree as a population of above ground N stem and branch sections where each section goes from one fork (or node) to the next – except for the bottom and top sections at which the tree begins and ends, respectively. From this set of N sections we would then select n sections as sample.
Doing so by simple random sampling (SRS), for example, we could directly estimate the mean bark volume per section. However, for estimation of the total, we would then face the problem that we needed to know the population size, i.e. the total number of sections to determine the expansion factor to extrapolate the mean section estimate to the whole tree. If the population size is known, we also know the inclusion probability for each section ‑ 1/N for simple random sampling ‑: this probability is required to develop an unbiased estimator for any design based sampling strategy. This is what we call probabilistic sampling.
In addition, to be able to carry out simple random selection, we also need to define the sampling frame so that we can unambiguously identify individual sampling elements sections, in our case). Both tasks (finding the population size and then defining the sampling frame), are clearly impractical for estimating total tree bark utilizing a simple random sampling approach.
Randomized branch sampling (RBS) is a sampling strategy that facilitates the drawing of a probabilistic sample without a priori defining the sampling frame. The inclusion probabilities of the selected population elements are determined in the course of the sampling process itself. RBS was developed by Jessen (1955)[1] for estimation of fruit count in orchards and has since been successfully applied to estimation of various tree variables (e.g. Valentine et al. 1984[2], Gregoire et al. 1995[3], Good et al. 2001[4], Cancino 2003, Cancino and Saborowski 2005[5]).
The principle of RBS can be visualized as a randomized unidirectional walk on a path along the network of stem sections starting from the bottom of the tree or another defined starting point to a defined end point (in our case up to a minimum branch diameter of 5 cm). Going along the path, at each fork a probability-based decision (utilizing random number tables or dice) is made to select the branch along which to proceed. Therefore, for each fork, the inclusion probability qi for the next section i is known. This permits the calculation of the overall selection probability for each section within the path as the product of the inclusion probabilities of all preceding sections. In Figure 3, for illustration, the marked outmost section has selection probability \(p_3 = q_1 * q_2 * q_3\). In that case, the first section (the stem) has an inclusion probability \(q_0 =1\) and therefore also \(p_0 = 1\) because that section is part of all possible sample paths.
Knowing the inclusion probability for each section of a path, an estimator for the total of the target variable can be developed using the Hansen-Hurwitz estimator. The total \(\tau\) can then be estimated from one path of m sections \(y_i\) selected with probabilities \(p_i\) by
\[ \hat \tau = \frac {1}{m} \sum_{i=1}^m \frac {y_i}{p_i}\]
| Figure 4. Illustration of estimation in randomized branch sampling (after Good et al. 2001[4]): for each section level, the observed value (bold rectangle) is expanded to an estimated total value by dividing that value by its selection probability which is indicated here by the arrows. The sum of all expanded values is the estimation of the tree´s total. The stem has selection probability 1 so that no expansion takes place. Obs: The heights of the sections are set equal here while, of course, they vary within and between sections. The width of the section levels is set to 100% here; the absolute values would also vary. | 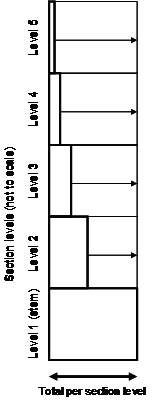
|
Following statistical sampling principles one path provides one independent observation. This observation is composed of several “sub‑observations”, the sections. This is the same principle which is also applied in Bitterlich sampling, where from one sample point various sample trees are included with probability proportional to their basal area; the sample tree values are then combined to one sample point observation by weighting them according to their individual inclusion probabilities. For randomized branch sampling the estimation mechanism is illustrated in Figure 4: dividing the observed section value by its per-section selection probability provides an estimation of the total on this section level (Good et al. 2001[4]).
If one path constitutes a sample of size n = 1, then more paths need to be selected per tree if estimation of precision is an issue. From n selected paths we generate n bark volume estimations \( \hat V_j\) the mean of which is taken as best estimate
\[\bar V = \frac {1}{n} \sum_{j=1}^n \hat V_j \]
with estimated variance
\[v\hat ar (\bar V) = \frac {s^2}{n} = \frac {1}{n} \frac {\sum_{j=1}^n (\hat V_j - \bar V)^2}{(n-1)}\]
[edit] References
- ↑ Jessen R.J. 1955. Determining the fruit count on a tree by randomized branch sampling. Biometrics 11:99-109
- ↑ Valentine TV, LM Tritton and GM Furnival. 1984. Subsampling Trees for Biomass, Volume or Mineral Content. Forest Science 30(3):673-681
- ↑ Gregoire TG, HT Valentine and GM Furnival. 1995. Sampling methods to estimate foliage and other characteristics of individual trees. Ecology 76:1181-1194
- ↑ 4.0 4.1 4.2 Good NM, M Paterson, C Brack and .K Mengersen. 2001. Estimating Tree Component Biomass Using Variable Probability Sampling Methods. Journal of Agricultural, Biological, and Environmental Statistics 6(2):258–267
- ↑ Cancino J and J Saborowski. 2005. Comparison of randomized branch sampling with and without replacement at the first stage. Silva Fennica 39(2):201-216.