Bitterlich sampling
Contents |
Angle count sampling was developed by Walter Bitterlich (1947/48), an Austrian forester (Bitterlich 1947 [2]). It is some times also referred to point sampling, horizontal point sampling, variable plot sampling, angle count technique, prism cruising, angle gauge sampling, and simply Bitterlich sampling.
The idea to employ nested sub-plots was introduced because we wished to have a balanced number of trees in all dimension classes; that is, we wanted to assign a higher probability of selection to the larger trees of which there are usually less in a stand (see also sampling with unequal selection probabilities).
For nested sub-plots, we defined a number of fixed plot areas in which the different dimension classes are observed. One may now further pursue that idea and develop a plot design in which the inclusion probability is strictly proportional to dimension. That is each tree has its particular and own plot size (and therefore also its particular inclusion zone). This is exactly what Bitterlich sampling does: from a selected sample point, the neighboring trees are selected strictly proportional to their basal area.
While this sounds complicated, the technique itself is very simple; the only device one needs is one that produced a defined opening angle. That can be a dendrometer, a relascope, a wedge prism or simply your own thumb. While standing on the sample point and aiming over e.g. the thumb at the stretched out arm to the dbhs of the surrounding trees; you sweep around 360° and count all trees that appear larger than your thumb. It is obvious then, that larger trees have a larger probability of being taken as sample tree. From this counting alone you can produce then an estimate of basal area per hectare.
The only additional information that you need is the “calibration factor” of your measurement device, as, obviously, the number of trees counted depends on the opening angle which is produced by the instrument (in this case by your arm length and thumb width).
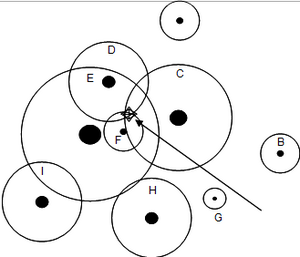
This calibration factor is also called basal area factor. Figure 1 illustrates that approach. Around each tree the individual inclusion zone is drawn. Sample points that fall into this inclusion zone will lead to an inclusion of this particular tree as sample tree. We may also imagine that these specific circular inclusion zones are concentrically placed around the sample point; then we may view them as a set of nested sample sub-plots, one for each sample tree.
The principle of Bitterlich sampling
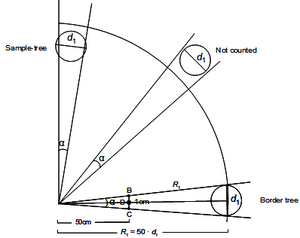


In a first step of developing this technique we need to calculate the size of these tree‑specific virtual sample plots. For each tree it holds the statement that it is only counted (or included) if it appears at 1.3 m height larger than the opening angle of the measurement device. For each tree there are exactly three different situations as depicted in Figure 2: (1) either the tree is larger than the opening angle; then the tree is inside the virtual nested sub-plot and is counted; or (2) the tree is smaller than the opening angle (that is: completely covered by the thumb); that is a non-tally tree which is outside the virtual plot; or (3) the tree is exactly covered by the opening angle; then, the tree is exactly on the perimeter line of the virtual circular plot and the distance from the sample point to the center of that tree is (for practical purposes sufficiently good approximation to) the radius of the virtual circular plot. We need to find this radius, because the virtual plot will allow us to calculate the tree-specific expansion factor that we need to expand the per-plot observation to the per-hectare observation.
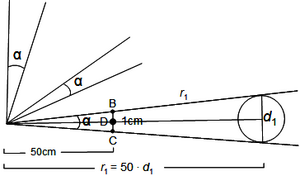
The opening angle can be produced by means of a stick of length c and a horizontal panel of width 1 cm at the end (analogous to arm and thumb, for example). For the virtual circle plot, for which this angle covers exactly a tree of dbh \(d_i\) (Figure 2) as a borderline tree, we obtain (approximately) plot radius \(r\) and plot area \(F_i\) along:
\[\frac{d_i}{r_i}=\frac{1}{c}\]
and then
\[r=cd_i\,\]
\[F_i={\pi}r^2={\pi}c^2{d_i}^2\,\]
This is then the virtual plot in which all trees with exactly the dbh \(d_i\) are tallied.
This corresponds exactly to the procedure with nested circular plots where also only a defined size class was observed in each nested sub-plot. If we count \(n_i\) trees with exactly the diameter \(d_i\) (or in diameter class \(d_i\) in case that we work with diameter classes) at a sample point, then these trees have the basal area
\[{n_i}{g_i}=n_i\frac{\pi}{4}{d_i}^2\,\]
Now, let’s expand this per-plot observation to a per-hectare figure (referring to trees with dbh \(d_i\) only!): the expansion factor is \(10000/F_i\), as usual, where \(F_i\) is the area of the virtual plot. The basal area per hectare for the trees of diameter \(d_i\) is then
\[G_{iHa}=\frac{10000}{F_i}n_i\frac{\pi}{4}{d_i}^2=\frac{10000}{\pi{c}^2{d_i}^2}n_i\frac{\pi}{4}{d_i}^2=\frac{2500}{c^2}n_i\,\]
Subsequently, this is done for all dbh-”classes” \(d_i\) and summed up to produce the estimate for the total basal area per hectare comprising all \(d\) classes:
\[G_{iHa}=\sum_{i}G_i=\frac{2500}{c^2}\sum_{i}n_i=\frac{2500}{c^2}N\,\]
where \(G_{Ha}\) = basal area per hectare of all trees. The only variable in that equation is
\[N=\sum_{}n_i\,\]
the number of observed/counted trees on the plot (over all diameter classes). This number of counted trees is multiplied with the factor
\[k=\frac{2500}{c^2}\,\]
which converts eventually the mere count into a basal-area-per-hectare value. This factor is called basal area factor and commonly denoted with \(k\). It is a factor that depends exclusively on the opening angle which is used.
By simply counting the \(N\) trees that are wider than our opening angle we can therefore produce an observation of basal area per hectare from a sample point:
\[G_{Ha}=k*N\,\]
It must be observed, however, that only basal area per hectare can be observed as simple as that. For all other variable that may be of interest (such as mean diameter or number of stems), in addition the dbhs of all trees need to be measured. That is explained further below.
Basal area factors can be different. Table 1 gives the lengths \(c\) of this stick for basal area factors of 1,2,3 and 4 when there is a panel of 1 cm at the end of a that stick. Following the above formula, the length of that stick is calculated by
\[c=\frac{50}{\sqrt{k}}\,\]
Table 1. Length \(c\) of the stick with 1cm for different values of the basal area factor \(k\)
Basal area factor (\(m^2/ha\)) c-value \(k=1m^2\,\) \(50\,\) \(k=2m^2\,\) \(35.4\,\) \(k=3m^2\,\) \(28.9\,\) \(k=4m^2\,\) \(25.0\,\)
Exact solution
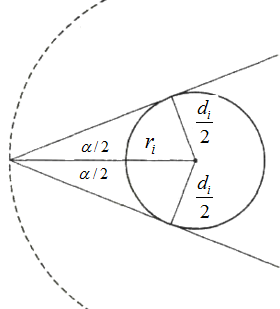
The principle presented above is, of course, only approximately correct, because the distance between the points at the tree where the viewing beams touch the tree is not exactly the tree diameter. For a geometrically correct calculation we would need to take that into account. The true distance between these two points is always shorter than \(d_i\). Figure 4 illustrates that and is gives the basis for the following calculations.
From Figure 4 we have
\[\mbox{sin }\frac{\alpha}{2}=\frac{\frac{d_i}{2}}{r_i}\,\]
and
\[r_i=\frac{d_i}{2*\mbox{sin }\frac{\alpha}{2}}.\,\]
The area of the virtual circular plot for the tree with diameter \(d_i\) is
\[A=\pi*r^2=\pi\frac{{d_i}^2}{4\left(\mbox{sin }\frac{\alpha}{2}\right)^2}\,\]
and the basal area per hectare results then from
\[G_i=10000*\frac{n_i*\frac{\pi}{4}*{d_i}^2}{\pi* \frac{{d_i}^2}{4*\left(\mbox{sin }\frac{\alpha}{2}\right)^2}}=10000*n_i*\left(\mbox{sin }\frac{\alpha}{2}\right)^2.\,\]
Basal area per hectare (of all trees) is then
\[G_{ha}=1000*\left(\sin\frac{\alpha}{2}\right)^2*\sum_{i=1}^k n_i,\,\]
where,
\[10000*\left(\sin\frac{\alpha}{2}\right)^2=k.\,\]
Therefore,
\[\sin\frac{\alpha}{2}=\frac{\sqrt{k}}{100}.\,\]
This is the mathematically correct derivation. However, the differences to the approximate solution as given above are so small that they can be accepted. The following gives the results of the simplified approximate calculation of the length \(c\) and the correct value \(c_c\):
\(k=1m^2\,\) \(c_c=49.997\,\) instead of \(c=50\,\) \(k=2m^2\,\) \(c_c=35.352\,\) instead of \(c=35.355\,\) \(k=4m^2\,\) \(c_c=24.995\,\) instead of \(c=25\,\)
Anyway, for all the calculations, we need to make the assumption that the tree’s cross section is a perfect circle; which it is not; so that there are more sources of geometrical inaccuracies than the one described here.
Choice of basal area factor
The choice of the basal area factor (\(k\)) in Bitterlich sampling is equivalent to the choice of plot size for fixed radius plot sampling. The criteria to be considered in the choice of basal area factor are visibility in the stand and average number of sample trees desired at a sample point. A decrease in the basal area factors increases the average number of sample trees tallied in. But that means also that trees at a farther distance to the sample point will be tally-trees. This will work smoothly only when visibility is accordingly
In high density stands higher BAF values such as \(4 m^2/ha\) are used. In low density stands with good visibility, low BAF values such as \(1 m^2/ha\) is normally used. In temperate and boreal regions basal area factors of 1 or 2 are common; in dense tropical rain forest values of \(9 m^2/ha\) may be appropriate.
 Note:
Note:
- The choice of a basal area factor refers to the entire sampling study (or in case of stratified sampling to the whole stratum). From a statistical point of view it is in principle not allowed to choose a different factor at each sampling location. Choosing a different plot size or counting factor depending on local density, would implicitly define multiple populations. This would mean the inclusion probability of a single tree would not be fixed anymore, but depending on the the local density around a sampling location. Such approaches are a matter of adaptive designs that might be notorious difficult in regard to unbiased estimators!
Of course, the target precision of a sampling study is always also an issue. With smaller values of \(k\) there will be more trees per sample plot (which comes together with somewhat higher cost) and with the same sample size, one will produce a higher precision than for larger values of \(k\).
Bitterlich sampling on sloped terrain
As in sampling with fixed area plots, all area measures in angle count sampling are assumed to be in the map plane. When applying Bitterlich sampling in sloped terrain we need to take the slope into account; either by using an instrument that does the correction automatically, or by introducing the correction factor into the analysis if the slope is not automatically corrected (which is the case, for example, if using a stick with a panel, or the thumb); this slope correction is then to be applied from slopes of 10% and more. The correction factor is
\[\frac{1}{\cos\alpha}\,\]
so that the basal area per hectare observation from one Bitterlich sample point is
\[G_i=k*N_i\frac{1}{\cos\alpha_i}\,\]
where:
\(G_i=\,\) corrected basal area (\(m^2/ha\)) at the \(i^{th}\) sampling point \(N_i=\,\) number of trees tallied at the sampling point and \(\alpha_i=\,\) angle of slope at the \(i^{th}\) sampling point.
Inclusion probabilities and estimators for Bitterlich sampling
For the inclusion zone approach where for each tree an inclusion zone is defined, see the corresponding article Infinite population approach. If used,the inclusion probability is then proportional to the size of this inclusion zone – which actually defines the probability that the correspondent tree is included in a sample.
We saw, for example, that angle count sampling (Bitterlich sampling) selects the trees with a probability proportional to their basal area and we emphasized that this fact makes Bitterlich sampling so efficient for basal area estimation. In contrast, point to tree distance sampling, or k-tree sampling, has inclusion zones that do not depend on any individual tree characteristic but only on the spatial arrangement of the neighboring trees; therefore, point-to tree distance sampling is not particularly precise for any tree characteristic.
In Bitterlich sampling, the selection probability of a particular tree i results from the inclusion zone Fi and the size of the reference area, for example the hectare
\[\pi_i = \frac {F_i}{10000}\]
with the Horvitz-Thompson estimator, we have the total
\[\hat \tau = \sum_{i=1}^m \frac {y_i}{\pi_i}\]
for any tree attribute \(y_i\). Applied to estimating basal area \(y_i = g_i = \frac {\pi}{4} d_i^2\) and its per hectare estimation, we have
\[\hat \tau = \sum_{i=1}^m \frac {y_i}{\pi_i} = \sum_{i=1}^m \cfrac {\cfrac {\pi}{4} d_i^2}{\cfrac {F_i}{10000}}\]
and with \( F_i = \pi r_i^2 = \pi c^2 \, d_i^2\), we have the same as Bitterlich sampling
\[\hat \tau = \sum_{i=1}^m \frac {y_i}{\pi_i} = \sum_{i=1}^m \cfrac {\cfrac {\pi}{4} d_i^2}{\cfrac {\pi c^2 \, d_i^2}{10000}} = \frac {2500 \pi}{\pi c^2} \sum_{i=1}^m \frac {d_i^2}{d_i^2} = \frac {2500}{c^2} m\]
which is the estimated basal area per hectare from one sample point where m trees were tallied. The factor 2500/c² is the basal area factor.
Estimation of number of stems
Angle count sampling allows a very fast estimation of basal area per hectare by simply counting trees. This procedure alone, however, does not allow making estimations for other variables. If we are interested in estimating number of stems per hectare, for example, we need to measure the diameters of all counted trees in order to be able to explicitly calculate their virtual circle plots and to make a correct expansion of their per-plot values to the corresponding per-hectare values.
Each diameter has its own expansion factor, namely
\[EF_i=\frac{10000}{F_i},\,\]
where \(F_i\) is the area of the corresponding “virtual plot”. For example for \(d=30cm\) (and \(k=2\), that is, \(c=35.52\)), we get the following expansion factor:
\[EF_i=\frac{10000}{F_i}=\frac{10000}{\pi{c^2}{d_i}^2}=\frac{10000}{\pi{35.35}^2{0.3}^2}=28.29\,\]
That tree with diameter \(d_i=30cm\), counted from the particular sample point, represents 28.29 trees per hectare with that diameter class; and, because the basal area factor is \(k=2 m^2/ha\), this tree does also represent \(2m^2\) of basal area per hectare.
The calculation of \(EF_i\) needs to be done for all diameters found on a sample point. Each diameter represents a different number of trees per hectare. At the end, to determine the total number of trees per hectare, these values need to be added.
In some textbooks there is another (equivalent – but somewhat more complicated and less intuitive) derivation of number of stems per hectare: one determines how many trees per hectare are represented by one counted tree:
For \(k=2\) one single tree represents \(2m^2\) of basal area per hectare. The basal area of one tree of, for example, \(d=30cm\) is
\[g={\pi}r^2=0.0707m^2\,\]
It follows that one counted tree “stands for”
\[\frac{2.0}{0.0707}=28.29\] trees/ha
in this diameter class 30cm. Obviously, the result is the same as for the more consistent expansion factor approach.
If we are interested in calculating the mean diameter from a Bitterlich sample, we can not simply take the mean diameter of the sample trees (as we do it for fixed area plot sampling) but we first need to derive the diameter distribution by means of the diameter-wise expansion and then calculate the mean diameter from that distribution.
Example
Calculation of number of stems per hectare from one Bitterlich sample point.
In Bitterlich sampling, the estimation of number of stems can not be done with a simple extrapolation of the counted number of trees, but we need to take into account the different selection probabilities, that is, the different sizes of the virtual nested sample plots (which is equivalent to the different size of the selection areas).
Each sampled tree “represents” a different number of trees in its dbh class ‑ depending on its dbh. A small tree, if sampled, represents a much larger number of small trees than a large tree if sampled. The calculation is illustrated in Table 1 for one Bitterlich sample with \(baf=2\). 10 trees were observed with their respective dbh measured. dbh and baf allow calculating the diameter-specific virtual nested circular plot area from
\[F_i={\pi}c^2d_i^2\,\]
and, therefore, also the dbh-specific expansion factor. Each tree represents a certain number of trees per hectare and the sum of all those figures is the estimated number of trees per hectare from this one Bitterlich sample. If n sample plots were taken, then for each one, this calculation needs to be done. The standard error of the estimation of number of stems per hectare results then from the results of these n estimations per plot.
Table 1. Illustration of estimation of number of trees per hectare from one point-relascope sample with \(baf=2\).
dbh of sample tree Area of virtual circular
nested sub-plotExpansion factor from plot
to per-hectare values“represented” number of
stems per hectare10 39.27 254.65 254.65 12 56.55 176.84 176.84 15 88.36 113.18 113.18 16 100.53 99.47 99.47 18 127.23 78.60 78.60 21 173.18 57.74 57.74 23 207.74 48.14 48.14 36 508.94 19.65 19.65 42 692.72 14.44 14.44 61 1461.23 6.84 6.84 Total 869.54
In this example, the expansion factor is equal to the represented number of trees per hectare because the calculation has been done for each individual tree and not for dbh-classes in which there are more than one tree.
See also
Video:Walter Bitterlich, An invention goes around the world
Video:Walter Bitterlich, Eine Erfindung geht um die Welt
References
- ↑ 1.0 1.1 1.2 Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.
- ↑ Bitterlich, W. 1947. Die Winkelzählmessung. Allgemeine Forst- und Holzwirtschaftliche Zeitung 58:94ff
- ↑ Kramer H. and A. Akca. 1995. Leitfaden zur Waldmesslehre. 3rd edition. J.D. Sauerländers Verlag, Frankfurt. 266p.