Random selection
Simple random selection requires that the sampling elements are independently randomly selected. Randomization is a design component of sampling design. The estimators for simple random sampling are unbiased if selection had been done at random. This is why we call such an estimator design-unbiased, because unbiasedness comes from the sampling design. We do not need to make assumptions with respect to the population, as the estimator is unbiased regardless of the structure of the population of interest (Kleinn et al. 2007[1]).
Note:
- The lack of randomization cannot be compensated by increasing sample size!
Randomization is one of the most important prerequisite in the so-called class of designed-based sampling (as opposed to model based sampling, where validity comes from the model assumed and randomization is not strictly necessary). However, the spatial structure of the population does affect the precision of our estimates.
Random selection is an essential component of all design based sampling. In addition, it is the basis for all statistical inference and testing. Simple random sampling where random selection is used, is easy to implement as long as there is an explicit sampling frame (a list or a map) or known sampling units. Mistakes are frequently made because the term random (equal chance) is confused with haphazard (without any pattern) or with arbitrary (do whatever you wish …).
- Note:
- randomization follows very clear rules, equal selection probabilities being the core property. It is hardly possible to simulate a random selection on a map by closing the eyes and pointing to a point in the map. Because the guarantee is not given, that, when doing that very often, really all points are being sampled with equal frequencies.
Random numbers as used for randomization are generated by software called “random number generator”; this is a whole science for itself. If randomization has been applied in a study, it is a good practice to also report how it was carried out.
Example 1:
For the random selection of one out of 2500 numbered elements (1…2500) we draw the random number 0.54321. The drawn random number, multiplied by 2500, gives the number 1358 or the element to be selected.
Example 2:
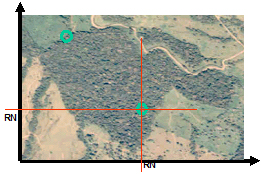
Random selection from an areal sampling frame: Figure 1 shows a forest patch with a selected sample plot to be inventoried. For the randome selection of this sample plot, one may apply the so called acceptance-rejection method which is illustrated in Figure 2. As we are on an areal sampling frame, two coordinates \((x, y)\) are required to define the exact sample location; and as a consequence we need two uniform random numbers \(u_1\) and \(u_2\) from the interval U[0.1]. With the help of the random numbers, the coordinates are drawn from the ranges of values in \(x\) and \(y\)-direction that encompasses the area of interest (i.e. \(x_{max}\) and \(y_{max}\)). Calculate \(x = u_1x_{max}\) and \(y = u_2y_{max}\). For the case that the point of origin is different from zero (e.g. some map units), just add the values of this point to the given equations \((x_{origin} , y_{origin})\).
If the coordinates (x,y) occur in the area of interest, then this point is accepted as a sample point; otherwise, the point is rejected and the procedure is repeated with two new random numbers.
References
- ↑ Kleinn, C.2007. Lecture Notes for the Teaching Module ForestInventory. Departmentof Forest Inventory and Remote Sensing. Facultyof Forest Science andForest Ecology, Georg-August-UniversitätGöttingen. 164 S.
