Horvitz-Thompson estimator
(Created page with "{{Content Tree|HEADER=Forest Inventory lecturenotes|NAME=Forest Inventory lecturenotes}} ==The Horvitz-Thompson estimator== Assuming that with any design, with or without repl...") |
|||
| (2 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Ficontent}} |
| − | + | Assuming that with any design, with or without replacement, the probability of including unit ''i'' in the sample is <math>\pi_i</math> (>0), for ''i=1,2,…, N''. The [[inclusion probability]] <math>\pi_i</math> can be calculated from the [[selection probability]] <math>p_i</math> and the corresponding complementary probability (1-''p<sub>i</sub>''), which is the probability that the element is not included into the sample at a particular draw. | |
| − | + | ||
| − | + | ||
| − | Assuming that with any design, with or without replacement, the probability of including unit ''i'' in the sample is <math>\pi_i</math> (>0), for ''i=1,2,…, N''. The inclusion probability <math>\pi_i</math> can be calculated from the selection probability <math>p_i</math> and the corresponding complementary probability (1-''p<sub>i</sub>''), which is the probability that the element is not included into the sample at a particular draw. | + | |
| − | + | ||
After ''n'' sample draws, the probability that element ''i'' is eventually included into the sample is <math>\pi</math>=1 - (1-''p<sub>i</sub>)<sup>n</sup>'', where (1 - ''p<sub>i</sub>'')<sup>''n''</sup> is the probability that the particular element is not included after ''n'' draws; the complementary probability to this is then the probability that the element is eventually in the sample (at least selected once). | After ''n'' sample draws, the probability that element ''i'' is eventually included into the sample is <math>\pi</math>=1 - (1-''p<sub>i</sub>)<sup>n</sup>'', where (1 - ''p<sub>i</sub>'')<sup>''n''</sup> is the probability that the particular element is not included after ''n'' draws; the complementary probability to this is then the probability that the element is eventually in the sample (at least selected once). | ||
| − | + | The Horvitz-Thompson estimator can be applied for sampling with or without replacement, but here it is illustrated for the case with replacement. | |
| − | The Horvitz-Thompson estimator can be applied for sampling with or without | + | |
| − | + | ||
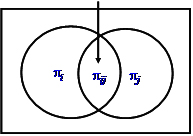
For the variance calculation with the Horvitz-Thompson estimator we also need to know the joint inclusion probability <math>\pi_{ij}</math> of two elements ''i'' and ''j'' after ''n'' sample draws, that is the probability that both ''i'' and ''j'' are eventually in the sample, after ''n'' draws. This joint inclusion probability is calculated from the two selection probabilities and the two inclusion probabilities after <math>\pi_{ij} = \pi_i + \pi_j - \{ 1 - (1 - p_i - p_j)^n \} </math> and can be illustrated as in Figure 1. | For the variance calculation with the Horvitz-Thompson estimator we also need to know the joint inclusion probability <math>\pi_{ij}</math> of two elements ''i'' and ''j'' after ''n'' sample draws, that is the probability that both ''i'' and ''j'' are eventually in the sample, after ''n'' draws. This joint inclusion probability is calculated from the two selection probabilities and the two inclusion probabilities after <math>\pi_{ij} = \pi_i + \pi_j - \{ 1 - (1 - p_i - p_j)^n \} </math> and can be illustrated as in Figure 1. | ||
| Line 16: | Line 10: | ||
[[image:SkriptFig_100.jpg|thumb|1000px|'''Figure 1.''' Diagram illustrating the joint inclusion probability.]] | [[image:SkriptFig_100.jpg|thumb|1000px|'''Figure 1.''' Diagram illustrating the joint inclusion probability.]] | ||
| − | |||
The Horvitz-Thompson estimator for the total is <math>\hat \tau = \sum_{i=1}^\nu \frac {y_i}{\pi_i}</math> | The Horvitz-Thompson estimator for the total is <math>\hat \tau = \sum_{i=1}^\nu \frac {y_i}{\pi_i}</math> | ||
| + | where the sum goes over the <math>\nu</math> distinct elements (where <math>\nu</math> is the Greek letter ''nu'') in the sample of size ''n'' (and not over all ''n'' elements) | ||
| − | + | The parametric [[error variance]] of the total is | |
| − | + | ||
| − | + | ||
| − | The parametric error variance of the total is | + | |
| − | + | ||
:<math>var(\hat \tau)=\sum_{i=1}^\nu \left (\frac {1 - \pi_i}{\pi_i} \right ) y_i^2 + \sum_{i=1}^N \sum_{j \ne i} \left (\frac {\pi_{ij} - \pi_i \pi_j}{\pi_i \pi_j} \right ) y_i y_j</math> | :<math>var(\hat \tau)=\sum_{i=1}^\nu \left (\frac {1 - \pi_i}{\pi_i} \right ) y_i^2 + \sum_{i=1}^N \sum_{j \ne i} \left (\frac {\pi_{ij} - \pi_i \pi_j}{\pi_i \pi_j} \right ) y_i y_j</math> | ||
| − | |||
which is estimated by | which is estimated by | ||
| − | |||
:<math>v\hat ar(\hat \tau)=\sum_{i=1}^\nu \left (\frac {1 - \pi_i}{\pi_i^2} \right ) y_i^2 + \sum_{i=1}^N \sum_{j \ne i} \left (\frac {\pi_{ij} - \pi_i \pi_j}{\pi_i \pi_j} \right ) \frac {y_i y_j}{\pi_{ij}}</math> | :<math>v\hat ar(\hat \tau)=\sum_{i=1}^\nu \left (\frac {1 - \pi_i}{\pi_i^2} \right ) y_i^2 + \sum_{i=1}^N \sum_{j \ne i} \left (\frac {\pi_{ij} - \pi_i \pi_j}{\pi_i \pi_j} \right ) \frac {y_i y_j}{\pi_{ij}}</math> | ||
| − | |||
A simpler (but slightly biased) approximation for the estimated error variance of the total is | A simpler (but slightly biased) approximation for the estimated error variance of the total is | ||
| − | |||
:<math>v\hat ar(\hat \tau) = \frac {N - \nu}{N} \frac {1}{\nu} \frac {\sum_{i=1}^\nu (\tau_i -\hat \tau)^2}{\nu - 1}</math> | :<math>v\hat ar(\hat \tau) = \frac {N - \nu}{N} \frac {1}{\nu} \frac {\sum_{i=1}^\nu (\tau_i -\hat \tau)^2}{\nu - 1}</math> | ||
| − | + | where <math>\tau_i</math> is the estimation for the total that results from each of the <math>\nu</math> sample. | |
| − | where | + | |
| Line 49: | Line 34: | ||
|text=application example | |text=application example | ||
}} | }} | ||
| − | |||
| − | |||
==References== | ==References== | ||
Latest revision as of 13:22, 26 October 2013
Assuming that with any design, with or without replacement, the probability of including unit i in the sample is \(\pi_i\) (>0), for i=1,2,…, N. The inclusion probability \(\pi_i\) can be calculated from the selection probability \(p_i\) and the corresponding complementary probability (1-pi), which is the probability that the element is not included into the sample at a particular draw.
After n sample draws, the probability that element i is eventually included into the sample is \(\pi\)=1 - (1-pi)n, where (1 - pi)n is the probability that the particular element is not included after n draws; the complementary probability to this is then the probability that the element is eventually in the sample (at least selected once).
The Horvitz-Thompson estimator can be applied for sampling with or without replacement, but here it is illustrated for the case with replacement.
For the variance calculation with the Horvitz-Thompson estimator we also need to know the joint inclusion probability \(\pi_{ij}\) of two elements i and j after n sample draws, that is the probability that both i and j are eventually in the sample, after n draws. This joint inclusion probability is calculated from the two selection probabilities and the two inclusion probabilities after \(\pi_{ij} = \pi_i + \pi_j - \{ 1 - (1 - p_i - p_j)^n \} \) and can be illustrated as in Figure 1.
The Horvitz-Thompson estimator for the total is \(\hat \tau = \sum_{i=1}^\nu \frac {y_i}{\pi_i}\)
where the sum goes over the \(\nu\) distinct elements (where \(\nu\) is the Greek letter nu) in the sample of size n (and not over all n elements)
The parametric error variance of the total is
\[var(\hat \tau)=\sum_{i=1}^\nu \left (\frac {1 - \pi_i}{\pi_i} \right ) y_i^2 + \sum_{i=1}^N \sum_{j \ne i} \left (\frac {\pi_{ij} - \pi_i \pi_j}{\pi_i \pi_j} \right ) y_i y_j\]
which is estimated by
\[v\hat ar(\hat \tau)=\sum_{i=1}^\nu \left (\frac {1 - \pi_i}{\pi_i^2} \right ) y_i^2 + \sum_{i=1}^N \sum_{j \ne i} \left (\frac {\pi_{ij} - \pi_i \pi_j}{\pi_i \pi_j} \right ) \frac {y_i y_j}{\pi_{ij}}\]
A simpler (but slightly biased) approximation for the estimated error variance of the total is
\[v\hat ar(\hat \tau) = \frac {N - \nu}{N} \frac {1}{\nu} \frac {\sum_{i=1}^\nu (\tau_i -\hat \tau)^2}{\nu - 1}\]
where \(\tau_i\) is the estimation for the total that results from each of the \(\nu\) sample.
 Horvitz-Thompson estimator example: application example
Horvitz-Thompson estimator example: application example