Simple random sampling
m (→Notations used) |
m (→Notations used) |
||
| Line 21: | Line 21: | ||
|Mean | |Mean | ||
|<math>\mu = \frac{\sum_{i=1}^N y_i}{N}</math> | |<math>\mu = \frac{\sum_{i=1}^N y_i}{N}</math> | ||
| − | |<math>\bar {y} = \frac{sum_{i=1}^n y_i}{n}</math> | + | |<math>\bar {y} = \frac{\sum_{i=1}^n y_i}{n}</math> |
|- | |- | ||
|Variance | |Variance | ||
Revision as of 12:24, 5 December 2010
Contents |
General observations
Simple random sampling (SRS) is the basic theoretical sampling technique. The sampling elements are selected as an independent random sample from the population. Each element of the population has the same probability of being selected. And, likewise, each combination of n sampling elements has the same probability of being eventually selected.
Every possible combination of sampling units from the population has an equal and independent chance of being in the sample.
Simple random sampling is introduced and dealt with here and in sampling textbooks mainly because it is a very instructive way to learn about sampling; many of the underlying concepts can excellently be explained with simple random sampling. However, it is hardly applied in forest inventories because there are various other sampling techniques which are more efficient, given the same sampling effort.
For information about how exactly sampling units are choosen see Random selection.
Notations used
Estimators Parametric Sample Mean \(\mu = \frac{\sum_{i=1}^N y_i}{N}\) \(\bar {y} = \frac{\sum_{i=1}^n y_i}{n}\) Variance \(\sigma^2 = \frac{\sum_{i=1}^N (y_i - \mu)^2}{N}\) \(s^2 = \frac{\sum_{i=1}^n (y_i - \bar {y})^2}{n-1}\) Standard deviation \(\sigma = \sqrt{\frac{\sum_{i=1}^N (y_i - \mu)^2}{N}}\) \(s = \sqrt{\frac{\sum_{i=1}^n (y_i - \bar {y})^2}{n-1}}\) Standard error (without replacement or from a finite population)
\(\sigma_{\bar {y}} = \sqrt{\frac{N-n}{N-1}}*\frac {\sigma}{\sqrt{n}}\) \(S_{\bar {y}} = \sqrt{\frac{N-n}{N}}*\frac{S_y}{\sqrt{n}}\) Standard error (with replacement or from an infinite population)
\(\sigma_{\bar {y}} = \frac{\sigma}{\sqrt{n}}\) \(S_{\bar {y}} = \frac{S_y}{\sqrt{n}}\)
- Where,
- \[N =\] number of sampling elements in the population (= population size);
- \[n =\] number of sampling elements in the sample (= sample size);
- \[y_i =\] observed value of i-th sampling element;
- \[\mu =\] parametric mean of the population;
- \[\bar {y} =\] estimated mean;
- \[\sigma =\] standard deviation in the population;
- \[S =\] estimated standard deviation in the population;
- \[\sigma^2 =\] parametric variance in the population;
- \[s^2 =\] estimated variance in the population;
- \[\sigma_{\bar {y}} =\] parametric standard error of the mean;
- \[s_{\bar {y}} =\] estimated standard error of the mean.
Examples
Example 1:
In this section, SRS estimators are illustrated with an example. This example will be pursued through the entire Lecture notes and illustrates that different sampling designs perform differently for the same population and with the same sample size.
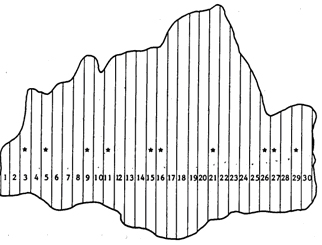
The example population has \(N = 30\) individual elements; we may imagine 30 strip plots that cover a forest area (Figure 73). This dataset will also be used in the further chapters for comparison among the performance of different sampling techniques.
Table 11 lists the values of the 30 units. Here, for SRS, we are only interested in the y values. The \(x\) values are a measure for the size (area) of the strips; this will later be used in the context of other estimators.
From this population we get the following parametric values:
\(\mu = \frac{\sum_{i=1}^N y_i}{N} = 7.0667\) and \(\sigma^2 = \frac{\sum_{i=1}^N (y_i - \mu)^2}{N} = 7.1289\)
If we take samples of size \(n=10\), then the parametric error variance of the estimated mean is:
\(var (\bar {y}) = \frac {N-n}{N-1} * \frac {\sigma^2}{n} = 0.491645\)
- Table 1:Example Population of N = 30 individual elements
Number y x 1 2 50 2 3 50 3 6 100 4 5 100 5 6 125 6 8 130 7 6 130 8 7 140 9 8 140 10 6 130 11 7 140 12 7 150 13 9 160 14 8 170 15 10 180 16 9 200 17 12 210 18 8 210 19 14 210 20 7 200 21 12 200 22 9 180 23 8 160 24 6 140 25 7 120 26 4 90 27 5 90 28 6 100 29 4 100 30 3 80 Mean 7.0667 13950 Pop. variance 7.1289 2087.25
This value will be compared in the subsequent chapters with the error variances produced by other sampling techniques with the same sample size \(n=10\). The square root of the error variance is the standard error; and this is the true parametric standard error which we strive to estimate from a single sample then. To recap: the parametric standard error is the standard deviation of all possible samples of size \(n=10\). In a concrete sampling study, we have only one single sample of size \(n=10\) and from this sample the standard error can only be estimated.
Example 2:
Let´s take one single sample of \(n=10\) from the population of \(N=30\) given in Figure 73 and Table 1. Assume that the following elements were randomly selected:
| sorry: |
This section is still under construction! This article was last modified on 12/5/2010. If you have comments please use the Discussion page or contribute to the article! |