Resource assessment exercises: fixed area plots
| Line 5: | Line 5: | ||
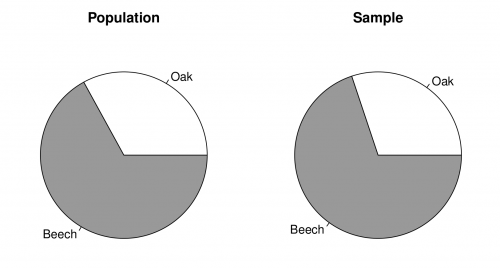
[[image:Resource_assessment_specshares.png|thumb|center|500px|'''Figure A:''' Pie chart of the species shares in the population (left) and in the sample (right).]] | [[image:Resource_assessment_specshares.png|thumb|center|500px|'''Figure A:''' Pie chart of the species shares in the population (left) and in the sample (right).]] | ||
| − | The “forest inventory” was conducted in [[:wikipedia:R_(programming_language)|R]]. The resulting dataset (as well as all other data we need in subsequent sections) is stored in the file | + | The “forest inventory” was conducted in [[:wikipedia:R_(programming_language)|R]]. The resulting dataset (as well as all other data we need in subsequent sections) is stored in the file MES.RData. We load the data into the workspace. |
<pre> | <pre> | ||
| Line 23: | Line 23: | ||
</pre> | </pre> | ||
| − | The variable | + | The variable plotID indicates on which plot the tree was found. How many trees are there on each of the 50 plots? |
<pre> | <pre> | ||
| Line 35: | Line 35: | ||
</pre> | </pre> | ||
| − | {{info|message=What the function | + | {{info|message=What the function table() does|text=The function table(x) provides the counts of unique values in a vector. E.g., table(fixed.area$stratum) would give us the number of trees sampled in each stratum.}} |
Suppose we would like to estimate the number of stems ha<math>^{-1}</math> in the forest. Since each plot covers an area of 0.08 hectares we need to compute the so-called plot expansion factor in order to be able to estimate the stems per hectare. If we have a radius of <math>r=15.45</math> the area covered by one plot is 750 m<math>^2</math>. | Suppose we would like to estimate the number of stems ha<math>^{-1}</math> in the forest. Since each plot covers an area of 0.08 hectares we need to compute the so-called plot expansion factor in order to be able to estimate the stems per hectare. If we have a radius of <math>r=15.45</math> the area covered by one plot is 750 m<math>^2</math>. | ||
| Line 58: | Line 58: | ||
</pre> | </pre> | ||
| − | {{info|message=Indexing using squared brackets | + | {{info|message=Indexing using squared brackets []|text= To access individual entries (or ranges of entries) in a vector we can use squared brackets. E.g. trees$dbh[2] selects the second value of dbh in trees. Instead of explicitly naming variables using the dollar sign, e.g., trees$dbh, we can also use the squared brackets. The principle is as follows: data.object[row(s), column(s)]. E.g., trees[c(1, 4:10), c(1,3)] would print out the first, fourth to tenth row, and the first and third column of trees.}} |
| − | The mean of | + | The mean of stems.ha.i provides a population estimate of the stems per hectare. |
<pre> | <pre> | ||
| Line 92: | Line 92: | ||
</pre> | </pre> | ||
| − | {{info|message=What the function | + | {{info|message=What the function unique() does|text= The function unique(x) reports the unique values in x. E.g., for a vector $1,2,2,3,3,3$, unique(c(1,2,2,3,3,3)) would print 1, 2, 3, the length would be three. }} |
We know the truth. | We know the truth. | ||
| Line 107: | Line 107: | ||
<pre> | <pre> | ||
| − | + | fixed.area$ba <- ((fixed.area$dbh/2)^2 * pi)/10000 | |
sum.ba <- tapply(fixed.area$ba, fixed.area$plotID, sum) | sum.ba <- tapply(fixed.area$ba, fixed.area$plotID, sum) | ||
ba.ha <- sum.ba * expf | ba.ha <- sum.ba * expf | ||
| Line 132: | Line 132: | ||
Finally, we estimate the proportion of beech trees in the forest. | Finally, we estimate the proportion of beech trees in the forest. | ||
| − | |||
| − | |||
<pre> | <pre> | ||
| + | fixed.area.beech <- fixed.area[fixed.area$species == 2, ] | ||
| + | n.beech.plot <- table(fixed.area.beech$plotID) | ||
| + | mean(n.beech.plot/n.trees) | ||
| + | |||
## [1] 0.6429 | ## [1] 0.6429 | ||
</pre> | </pre> | ||
| − | |||
| − | <code> | + | There is one plot (plotID 5) without any beech tree. One way to solve the problem would be use the <code>levels</code> argument of the <code>factor()</code> function. |
<pre> | <pre> | ||
| + | n.beech.plot <- table(factor(fixed.area.beech$plotID, levels = 1:50)) | ||
| + | (p <- mean(n.beech.plot/n.trees)) | ||
| + | |||
## [1] 0.6429 | ## [1] 0.6429 | ||
</pre> | </pre> | ||
| − | |||
| − | <code> | + | {{info|message=What the function <code>factor()</code> does|text=The function <code>factor(x)</code> is used to encode a vector into factor levels. The <code>levels</code> argument is used to specify the factor levels.}} |
| + | |||
| + | The estimated standard error is | ||
<pre> | <pre> | ||
| + | q <- 1 - p | ||
| + | sqrt((p * q)/(n - 1)) | ||
| + | |||
## [1] 0.06845 | ## [1] 0.06845 | ||
</pre> | </pre> | ||
| − | Figure | + | Figure '''A''' shows to pie charts of the proportion of beech trees in the population (left) and the sample (right). You can recreate the plots |
| + | with the following code: | ||
| − | < | + | <pre> |
| − | + | pie(table(trees$species), labels = c("Oak", "Beech"), main = "Population") | |
| − | + | pie(table(fixed.area$species), labels = c("Oak", "Beech"), main = "Sample") | |
| + | </pre> | ||
| − | |||
| − | == Exercises == | + | == Additional Exercises == |
* Load the file <code>exercises.RData</code> into the workspace. The file contains a <code>data.frame</code> named <code>fixed.area.Ex</code> that holds data from a forest inventory using fixed area sample plots. The size of the plot is 750 m<math>^2</math>. | * Load the file <code>exercises.RData</code> into the workspace. The file contains a <code>data.frame</code> named <code>fixed.area.Ex</code> that holds data from a forest inventory using fixed area sample plots. The size of the plot is 750 m<math>^2</math>. | ||
Revision as of 08:22, 23 July 2014
| sorry: |
This section is still under construction! This article was last modified on 07/23/2014. If you have comments please use the Discussion page or contribute to the article! |
Suppose a forest inventory has been conducted in the simulated 50 hectare forest. In total \(n=50\) fixed area sample plots with a radius of \(r=15.45\) meters have been randomly placed in the forest (see Figure A). The area covered by a single plot is 0.08 hectares. If parts of the plot lay outside the forest area, this part was mirrored back (see Kleinn (2013)[1] and this article for details). For all trees with a DBH \(\geq\) 5 cm the DBH (cm), height (m) and tree species was recorded. Furthermore the azimuth (1–360\(^\circ\)) and distance (m) of each tree to the plot center on which the tree was found was measured.
The “forest inventory” was conducted in R. The resulting dataset (as well as all other data we need in subsequent sections) is stored in the file MES.RData. We load the data into the workspace.
load("./data/MES.RData") # Don't forget to adjust the path!
str(fixed.area) # Data for the fixed area plots
## 'data.frame': 2158 obs. of 9 variables:
## $ plotID : num 1 1 1 1 1 1 1 1 1 1 ...
## $ plot.x : num 620753 620753 620753 620753 620753 ...
## $ plot.y : num 5886461 5886461 5886461 5886461 5886461 ...
## $ species : num 1 1 1 1 1 1 1 1 1 1 ...
## $ dbh : num 21 23 26 26 21 13 25 22 26 21 ...
## $ height : num 11.86 12.06 11.08 10.36 9.36 ...
## $ ab : num 0.1056 0.1292 0.152 0.1421 0.0831 ...
## $ azimuth : num 101.1 235.7 63.3 309.4 280 ...
## $ distance: num 12.22 12.75 8.05 9.52 13.98 ...
The variable plotID indicates on which plot the tree was found. How many trees are there on each of the 50 plots?
n.trees <- table(fixed.area$plotID) ## ## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 ## 47 63 92 46 42 66 52 66 49 74 79 52 48 40 30 56 67 51 59 60 45 44 49 76 35 33 ## 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 ## 25 37 29 36 31 39 54 20 24 27 21 25 38 32 37 31 39 16 20 36 29 33 21 37
 What the function table() does
What the function table() does
- The function table(x) provides the counts of unique values in a vector. E.g., table(fixed.area$stratum) would give us the number of trees sampled in each stratum.''
Suppose we would like to estimate the number of stems ha\(^{-1}\) in the forest. Since each plot covers an area of 0.08 hectares we need to compute the so-called plot expansion factor in order to be able to estimate the stems per hectare. If we have a radius of \(r=15.45\) the area covered by one plot is 750 m\(^2\).
expf <- 10000/750 # expansion factor for a plot of 750 square meters expf ## [1] 13.33
When we multiply the number of trees of each plot with the expansion factor we obtain the number of trees per hectare and plot.stems.ha.i <- n.trees * expf stems.ha.i[1:10] # to save space, only the first 10 plots are printed ## ## 1 2 3 4 5 6 7 8 9 10 ## 626.7 840.0 1226.7 613.3 560.0 880.0 693.3 880.0 653.3 986.7
;[[image:info.png|info.png]] '''Indexing using squared brackets []''' :''To access individual entries (or ranges of entries) in a vector we can use squared brackets. E.g. trees$dbh[2] selects the second value of dbh in trees. Instead of explicitly naming variables using the dollar sign, e.g., trees$dbh, we can also use the squared brackets. The principle is as follows: data.object[row(s), column(s)]. E.g., trees[c(1, 4:10), c(1,3)] would print out the first, fourth to tenth row, and the first and third column of trees.'' The mean of stems.ha.i provides a population estimate of the stems per hectare.mean(stems.ha.i) ## [1] 575.5
How good is our estimate (see [[Resource assessment exercises: standard error and confidence intervals|standard error and confidence intervals]])?(n <- length(unique(fixed.area$plotID))) # sample size ## [1] 50 (se <- sd(stems.ha.i)/sqrt(n)) # estimated standard error (SE) ## [1] 32.43 (relse <- se/mean(stems.ha.i) * 100) # relative SE in % ## [1] 5.636 mean(stems.ha.i) - se * qt(0.975, n - 1) # lower confidence limit ## [1] 510.3 mean(stems.ha.i) + se * qt(0,975, n - 1) # upper confidence limit ## [1] 640.6
;[[image:info.png|info.png]] '''What the function unique() does''' :''The function unique(x) reports the unique values in x. E.g., for a vector $1,2,2,3,3,3$, unique(c(1,2,2,3,3,3)) would print 1, 2, 3, the length would be three.
We know the truth.
stems.ha <- nrow(trees)/50 stems.ha ## [1] 600
Next, we estimate the BA ha\(^{-1}\). First, we need to calculate the BA (m\(^2\)) for each tree. Second, the total BA is calculated for each plot. Third, the results are multiplied with the expansion factor. Finally, the BA ha\(^{-1}\) is estimated for the forest.
fixed.area$ba <- ((fixed.area$dbh/2)^2 * pi)/10000 sum.ba <- tapply(fixed.area$ba, fixed.area$plotID, sum) ba.ha <- sum.ba * expf (ba.fixed.area.mean <- mean(ba.ha)) ## [1] 33.17
We estimate the relative standard error in percent:
(ba.fixed.area.ser <- sd(ba.ha)/sqrt(n)/mean(ba.ha) * 100) ## [1] 10.29
Thus, we expect the BA ha\(^{-1}\) to be 33.17 \(\pm\) 6.86 m\(^2\). The parametric BA ha\(^{-1}\) is,
sum(trees[, "ba"])/50 ## [1] 28.66
Finally, we estimate the proportion of beech trees in the forest.
fixed.area.beech <- fixed.area[fixed.area$species == 2, ] n.beech.plot <- table(fixed.area.beech$plotID) mean(n.beech.plot/n.trees) ## [1] 0.6429
There is one plot (plotID 5) without any beech tree. One way to solve the problem would be use the levels argument of the factor() function.
n.beech.plot <- table(factor(fixed.area.beech$plotID, levels = 1:50)) (p <- mean(n.beech.plot/n.trees)) ## [1] 0.6429
 What the function
What the function factor()does- The function
factor(x)is used to encode a vector into factor levels. Thelevelsargument is used to specify the factor levels.
The estimated standard error is
q <- 1 - p sqrt((p * q)/(n - 1)) ## [1] 0.06845
Figure A shows to pie charts of the proportion of beech trees in the population (left) and the sample (right). You can recreate the plots with the following code:
pie(table(trees$species), labels = c("Oak", "Beech"), main = "Population")
pie(table(fixed.area$species), labels = c("Oak", "Beech"), main = "Sample")
Additional Exercises
- Load the file
exercises.RDatainto the workspace. The file contains adata.framenamedfixed.area.Exthat holds data from a forest inventory using fixed area sample plots. The size of the plot is 750 m\(^2\). - Calculate the expansion factor for a plot.
- How large is \(n\) (
plotIDgives the plot number for each tree)? - Estimate the BA ha\(^{-1}\) and the number of stems per hectare. Provide an estimate of the standard error and construct confidence intervals for \(\alpha=0.10\).
Related articles
References
- ↑ Kleinn, C., 2013. Lecture Notes for the Teaching Module Forest Inventory.