Theodolite
(→Functional principle) |
|||
| (6 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
==Functional principle== | ==Functional principle== | ||
| − | A theodolite is used for measuring vertical and horizontal [[ | + | A theodolite is used for measuring vertical and horizontal [[angle|angles]]. The main parts are the horizontal and the vertical circles, which are scaled in [[gon]]. It is regularly placed on a [[:wikipedia:tripod|tripod]] and features several [[wikipedia:spirit level|spirit levels]] for adjusting the theodolite in the field. |
| − | A theodolite featuring a device for optical distance measurement is called ''tachymeter''. More modern tachymeters equipped with electrical distance measurement devices are called ''total | + | A theodolite featuring a device for optical distance measurement is called ''tachymeter''. More modern tachymeters equipped with electrical distance measurement devices are called ''total stations''. |
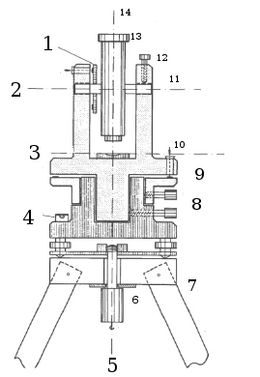
[[File:Theodolit.jpg|thumb|right|260px|Sketch of a theodolite with numbers indicating the functional parts. '''1:''' Vertical circle. '''2:''' Reading for vertical circle. '''3:''' Spirit level axis. '''4:''' Bulls eye spirit level. '''5:''' Plumb-bob. '''6:''' Fixation screw. '''7:''' Tripod. '''8:''' Clamps. '''9:''' Horizontal circle. '''10:''' Reading for horizontal circle. '''11:''' Horizontal axis (tilt axis). '''12:''' Clamp. '''13:''' Telescope. '''14:''' Vertical axis.]] | [[File:Theodolit.jpg|thumb|right|260px|Sketch of a theodolite with numbers indicating the functional parts. '''1:''' Vertical circle. '''2:''' Reading for vertical circle. '''3:''' Spirit level axis. '''4:''' Bulls eye spirit level. '''5:''' Plumb-bob. '''6:''' Fixation screw. '''7:''' Tripod. '''8:''' Clamps. '''9:''' Horizontal circle. '''10:''' Reading for horizontal circle. '''11:''' Horizontal axis (tilt axis). '''12:''' Clamp. '''13:''' Telescope. '''14:''' Vertical axis.]] | ||
==Measuring polygonal chains== | ==Measuring polygonal chains== | ||
| − | The choice of the points (vertices) of the polygonal chain depend on the aim of the mensuration. In most cases, one will follow the course of roads and trails. The single segments should be located in a way that other objects can be connected easily. The line segments should be relatively long, to keep the [[ | + | The choice of the points (vertices) of the polygonal chain depend on the aim of the mensuration. In most cases, one will follow the course of roads and trails. The single segments should be located in a way that other objects can be connected easily. The line segments should be relatively long, to keep the [[error propagation in polygon chain measurement|error propagation]] low - not less than 50 meters and, under normal circumstances, not more than 200 to 300 meters <ref name=kleinn09> Kleinn, Dr. C. Skriptum zur Vorlesung „Einführung in die Vermessungslehre“ für Studierende der Forstwissenschaften. Georg August Universität Göttingen, 2009. </ref>. |
To asses the absolute position of a polygon chain, it has to be connected to a trigonometric vertex close to it. Generally, close vertices should be part of the polygonal chain. | To asses the absolute position of a polygon chain, it has to be connected to a trigonometric vertex close to it. Generally, close vertices should be part of the polygonal chain. | ||
| Line 16: | Line 16: | ||
From each vertex, the distance to the preceding and to the following vertex is measured. The distance mensuration is done twice, the second measuring can be seen as safety mensuration. The mean of both mensurations is taken for the best approximation of the real distance. The distance is mostly obtained with electronic distance measurement tools. The [[Angles | angle of refraction]] between two distances can be derived from the difference between the two readings of the horizontal circle, obtained by the bearing to the preceding and to the following vertex. | From each vertex, the distance to the preceding and to the following vertex is measured. The distance mensuration is done twice, the second measuring can be seen as safety mensuration. The mean of both mensurations is taken for the best approximation of the real distance. The distance is mostly obtained with electronic distance measurement tools. The [[Angles | angle of refraction]] between two distances can be derived from the difference between the two readings of the horizontal circle, obtained by the bearing to the preceding and to the following vertex. | ||
| − | The [[Angles | | + | The [[Angles | angle of inclination]] is derived from the vertical circle reading. All measured parameters are recorded on a survey sheet. Additionaly, all vertices are plotted in a sketch map. |
If a polygon chain measured with a theodolite is to be drawn into a map, in at least one point the direction has to be measured (with a [[compass]]) to correctly fit it into the [[coordinate system]]<ref name=kleinn09> </ref>. | If a polygon chain measured with a theodolite is to be drawn into a map, in at least one point the direction has to be measured (with a [[compass]]) to correctly fit it into the [[coordinate system]]<ref name=kleinn09> </ref>. | ||
==Polar coordinate method== | ==Polar coordinate method== | ||
| − | This method can be applied in clearly arranged terrain. Measurement is conducted from one fixed point. The distance and the [[Angles|angle of refraction]] from the point are measured. Thus, it is basically a measurement of [[coordinates|polar coordinates]]. The distance is taken | + | This method can be applied in clearly arranged terrain. Measurement is conducted from one fixed point. The distance and the [[Angles|angle of refraction]] from the point are measured. Thus, it is basically a measurement of [[coordinates|polar coordinates]]. The distance is taken tachymetric or electronic. |
To draw the obtained vertices to a map, the coordinates of at least two points have to be available. | To draw the obtained vertices to a map, the coordinates of at least two points have to be available. | ||
| Line 31: | Line 31: | ||
<references/> | <references/> | ||
| − | [[category: | + | [[category:Survey]] |
Latest revision as of 14:21, 30 May 2011
Contents |
[edit] Functional principle
A theodolite is used for measuring vertical and horizontal angles. The main parts are the horizontal and the vertical circles, which are scaled in gon. It is regularly placed on a tripod and features several spirit levels for adjusting the theodolite in the field.
A theodolite featuring a device for optical distance measurement is called tachymeter. More modern tachymeters equipped with electrical distance measurement devices are called total stations.
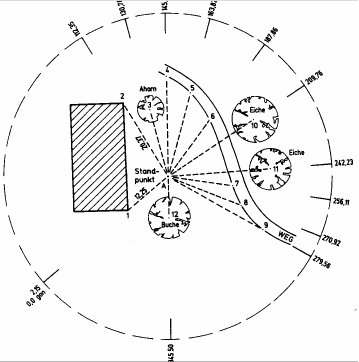
[edit] Measuring polygonal chains
The choice of the points (vertices) of the polygonal chain depend on the aim of the mensuration. In most cases, one will follow the course of roads and trails. The single segments should be located in a way that other objects can be connected easily. The line segments should be relatively long, to keep the error propagation low - not less than 50 meters and, under normal circumstances, not more than 200 to 300 meters [1].
To asses the absolute position of a polygon chain, it has to be connected to a trigonometric vertex close to it. Generally, close vertices should be part of the polygonal chain.
In the field, the procedure goes as follows: The individual vertices are to be marked with perpendicular ranging rods. The theodolite is centered exactly over the respective vertex. Both tasks are to be fulfilled with full attention to minimize errors in the angle measurement.
From each vertex, the distance to the preceding and to the following vertex is measured. The distance mensuration is done twice, the second measuring can be seen as safety mensuration. The mean of both mensurations is taken for the best approximation of the real distance. The distance is mostly obtained with electronic distance measurement tools. The angle of refraction between two distances can be derived from the difference between the two readings of the horizontal circle, obtained by the bearing to the preceding and to the following vertex.
The angle of inclination is derived from the vertical circle reading. All measured parameters are recorded on a survey sheet. Additionaly, all vertices are plotted in a sketch map.
If a polygon chain measured with a theodolite is to be drawn into a map, in at least one point the direction has to be measured (with a compass) to correctly fit it into the coordinate system[1].
[edit] Polar coordinate method
This method can be applied in clearly arranged terrain. Measurement is conducted from one fixed point. The distance and the angle of refraction from the point are measured. Thus, it is basically a measurement of polar coordinates. The distance is taken tachymetric or electronic. To draw the obtained vertices to a map, the coordinates of at least two points have to be available.
Today, this is the standard method for extensive measurements, as angle and distance measuring can be conducted automatically in most cases [2].