Resource assessment exercises: nested fixed area plots
| (5 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
In the last subsection we saw that we “measured” 2,158 DBHs on the <math>n=50</math> fixed area plots. Many of the trees are relatively small, i.e., have small DBHs. Figure '''A''' shows a histogram of the variable <code>dbh</code>. The bin width is two centimeters. | In the last subsection we saw that we “measured” 2,158 DBHs on the <math>n=50</math> fixed area plots. Many of the trees are relatively small, i.e., have small DBHs. Figure '''A''' shows a histogram of the variable <code>dbh</code>. The bin width is two centimeters. | ||
| Line 8: | Line 6: | ||
</pre> | </pre> | ||
| − | {{info|message=What the function <code>seq()</code> does|text=The function <code>seq(from, to, by)</code> creates a sequence of values. The argument <code>by</code> defines the step length. Alternatively you can use, e.g., <code>length.out</code>. For example <code>seq(0, 1, length.out = 10)} creates a sequence from zero to one of length 10. | + | {{info|message=What the function <code>seq()</code> does|text=The function <code>seq(from, to, by)</code> creates a sequence of values. The argument <code>by</code> defines the step length. Alternatively you can use, e.g., <code>length.out</code>. For example <code>seq(0, 1, length.out = 10)} creates a sequence from zero to one of length 10.</code>}} |
| Line 29: | Line 27: | ||
We see that many trees have a DBH below 15 cm. Measuring all the DBHs on a plot is often a tedious task. Moreover, small trees contribute relatively little to the BA ha<math>^{-1}</math>. Can we reduce the number of small trees we need to measure? | We see that many trees have a DBH below 15 cm. Measuring all the DBHs on a plot is often a tedious task. Moreover, small trees contribute relatively little to the BA ha<math>^{-1}</math>. Can we reduce the number of small trees we need to measure? | ||
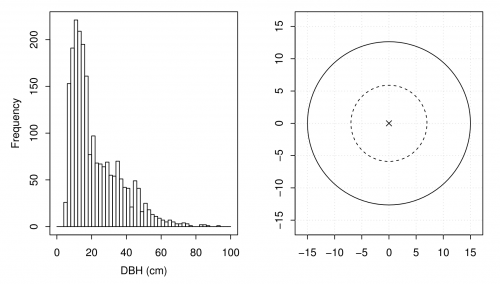
| − | In forest inventories nested plots are frequently used (see Figure | + | In forest inventories nested plots are frequently used (see Figure '''A'''). Within the larger area (solid line) all trees with a DBH larger than 15 centimeters are measured, and small trees (<math>\leq</math>15 cm) are only recorded within the smaller circle (dashed line). The radius of the smaller plot is <math>r_{\text{small}}=7.73</math> and for the larger we still use a radius of <math>r_{\text{large}}=15.45</math>. |
| − | + | The file <code>MES.RData</code> contains a <code>data.frame</code> named <code>nested</code>. The locations of the plots are exactly the same as for the <code>fixed.area</code> plots. However, we used a threshold diameter for small trees (<math>\leq</math>15 cm) in a nested plot design. | |
Here are the number of trees we measured. | Here are the number of trees we measured. | ||
<pre> | <pre> | ||
| + | nrow(nested) | ||
| + | |||
## [1] 1624 | ## [1] 1624 | ||
</pre> | </pre> | ||
<pre> | <pre> | ||
| + | nrow(fixed.area) | ||
| + | |||
## [1] 2158 | ## [1] 2158 | ||
</pre> | </pre> | ||
| + | |||
Using the nested plot design we reduced the number of measured DBHs by 534. Does it reduce the precision of the BA ha<math>^{-1}</math> estimate considerably? | Using the nested plot design we reduced the number of measured DBHs by 534. Does it reduce the precision of the BA ha<math>^{-1}</math> estimate considerably? | ||
| − | + | First, we need to calculate the BA for each tree again. Second, we need to calculate the expansion factors for the larger and smaller nested plot. | |
| − | + | ||
<pre> | <pre> | ||
| + | nested$ba <- (pi * (nested$dbh/2)^2)/10000 | ||
| + | Al <- 750 # area of the larger plot | ||
| + | (rl <- sqrt(750/pi)) # radius of a plot of size 750 square meters | ||
| + | |||
## [1] 15.45 | ## [1] 15.45 | ||
| − | |||
| − | < | + | (rs <- rl/2) # smaller radius is half the larger radius |
| + | |||
## [1] 7.725 | ## [1] 7.725 | ||
| − | |||
| − | < | + | (As <- pi * rs^2) # area of the (smaller) nested plot |
| + | |||
## [1] 187.5 | ## [1] 187.5 | ||
| + | |||
| + | ha <- 10000 # a hectare in square meters | ||
| + | expf.large <- ha/Al # expansion factor for large plots | ||
| + | expf.small <- ha/As # expansion factor for small plots | ||
</pre> | </pre> | ||
| − | + | Third, the BA per hectare and plot is calculated for the large and small plots and multiplied with the respective expansion factor. | |
| + | <pre> | ||
| + | bal <- tapply(nested[nested$dbh > 15, "ba"], | ||
| + | nested[nested$dbh > 15, "plotID"], sum) * expf.large | ||
| + | bas <- tapply(nested[nested$dbh <= 15, "ba"], | ||
| + | nested[nested$dbh <= 15, "plotID"], sum) * expf.small | ||
| + | </pre> | ||
Finally, we sum up the BA ha<math>^{-1}</math> for large and small plots. | Finally, we sum up the BA ha<math>^{-1}</math> for large and small plots. | ||
| + | <pre> | ||
| + | ba.ha <- bal + bas | ||
| − | + | ## Error: non-conformable arrays | |
| + | </pre> | ||
The error message is printed because there are small plots that do not contain any trees, i.e., <code>bal</code> and <code>bas</code> do not have the same length. Here is a simple workaround. | The error message is printed because there are small plots that do not contain any trees, i.e., <code>bal</code> and <code>bas</code> do not have the same length. Here is a simple workaround. | ||
| + | <pre> | ||
| + | nested$plotID <- as.factor(nested$plotID) | ||
| + | |||
| + | bal <- tapply(nested[nested$dbh > 15, "ba"], | ||
| + | nested[nested$dbh > 15, "plotID"], sum) * expf.large | ||
| + | bas <- tapply(nested[nested$dbh <= 15, "ba"], | ||
| + | nested[nested$dbh <= 15, "plotID"], sum) * expf.small | ||
| + | bal[is.na(bal)] <- 0 | ||
| + | bas[is.na(bas)] <- 0 | ||
| + | ba.ha <- bal + bas | ||
| + | </pre> | ||
Next, we compute the mean of the BA ha<math>^{-1}</math> per plot to estimate the population BA ha<math>^{-1}</math>. | Next, we compute the mean of the BA ha<math>^{-1}</math> per plot to estimate the population BA ha<math>^{-1}</math>. | ||
| − | |||
<pre> | <pre> | ||
| + | (ba.nested.mean <- mean(ba.ha)) | ||
| + | |||
## [1] 34.62 | ## [1] 34.62 | ||
</pre> | </pre> | ||
| + | |||
Finally, we construct the confidence intervals around our estimated mean. | Finally, we construct the confidence intervals around our estimated mean. | ||
| + | <pre> | ||
| + | ba.nested.se <- sd(ba.ha)/sqrt(n)) | ||
| − | |||
## [1] 3.245 | ## [1] 3.245 | ||
| − | |||
| − | < | + | (ba.nested.ser <- sd(ba.ha)/sqrt(n)/mean(ba.ha) * 100) |
| + | |||
## [1] 9.376 | ## [1] 9.376 | ||
| − | |||
| − | < | + | (conf <- ba.nested.se * qt(0.975, n - 1)) |
| + | |||
## [1] 6.522 | ## [1] 6.522 | ||
| − | |||
| − | + | mean(ba.ha) - conf | |
| + | |||
## [1] 28.09 | ## [1] 28.09 | ||
| − | |||
| − | + | mean(ba.ha) + conf | |
| + | |||
## [1] 41.14 | ## [1] 41.14 | ||
</pre> | </pre> | ||
| − | |||
| + | |||
| + | == Additional exercises == | ||
Repeat the tasks from the last exercise (Section [sub:fixedex]). Use the data in <code>nested.Ex</code>. Trees with a DBH <math>\leq</math> 15 cm have only been measured within a smaller circular plot with <math>r=10</math> meters. | Repeat the tasks from the last exercise (Section [sub:fixedex]). Use the data in <code>nested.Ex</code>. Trees with a DBH <math>\leq</math> 15 cm have only been measured within a smaller circular plot with <math>r=10</math> meters. | ||
| + | |||
| + | == Related articles == | ||
| + | * Previous article: [[Resource assessment exercises: fixed area plots|fixed area plots]] | ||
| + | * Next article: [[Resource assessment exercises: k-tree sampling|k-tree sampling]] | ||
| + | |||
| + | [[category:Response designs in resource assessment (2014)|Nested fixed area plots]] | ||
Latest revision as of 14:01, 23 July 2014
In the last subsection we saw that we “measured” 2,158 DBHs on the \(n=50\) fixed area plots. Many of the trees are relatively small, i.e., have small DBHs. Figure A shows a histogram of the variable dbh. The bin width is two centimeters.
bins <- seq(from=0, to=100, by=2) # define bin wiedth (here, 2 cm classes) hist(fixed.area$dbh, breaks=bins, main="", xlab="DBH (cm)")
 What the function
What the function seq()does- The function
seq(from, to, by)creates a sequence of values. The argumentbydefines the step length. Alternatively you can use, e.g.,length.out. For exampleseq(0, 1, length.out = 10)} creates a sequence from zero to one of length 10.
We use the quantile() function to obtain a numerical representation of the DBH distribution.
quantile(fixed.area$dbh, probs=seq(from=0, to=1, by=0.1)) ## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ## 6 9 11 13 15 17 22 28 35 45 93
 What the function
What the function quantile()does- The function
quantile(x, )provides sample quantiles for given probabilities (argumentprobs). The probabilities have lie between zero and one, i.e., [0, 1].
We see that many trees have a DBH below 15 cm. Measuring all the DBHs on a plot is often a tedious task. Moreover, small trees contribute relatively little to the BA ha\(^{-1}\). Can we reduce the number of small trees we need to measure?
In forest inventories nested plots are frequently used (see Figure A). Within the larger area (solid line) all trees with a DBH larger than 15 centimeters are measured, and small trees (\(\leq\)15 cm) are only recorded within the smaller circle (dashed line). The radius of the smaller plot is \(r_{\text{small}}=7.73\) and for the larger we still use a radius of \(r_{\text{large}}=15.45\).
The file MES.RData contains a data.frame named nested. The locations of the plots are exactly the same as for the fixed.area plots. However, we used a threshold diameter for small trees (\(\leq\)15 cm) in a nested plot design.
Here are the number of trees we measured.
nrow(nested) ## [1] 1624
nrow(fixed.area) ## [1] 2158
Using the nested plot design we reduced the number of measured DBHs by 534. Does it reduce the precision of the BA ha\(^{-1}\) estimate considerably?
First, we need to calculate the BA for each tree again. Second, we need to calculate the expansion factors for the larger and smaller nested plot.
nested$ba <- (pi * (nested$dbh/2)^2)/10000 Al <- 750 # area of the larger plot (rl <- sqrt(750/pi)) # radius of a plot of size 750 square meters ## [1] 15.45 (rs <- rl/2) # smaller radius is half the larger radius ## [1] 7.725 (As <- pi * rs^2) # area of the (smaller) nested plot ## [1] 187.5 ha <- 10000 # a hectare in square meters expf.large <- ha/Al # expansion factor for large plots expf.small <- ha/As # expansion factor for small plots
Third, the BA per hectare and plot is calculated for the large and small plots and multiplied with the respective expansion factor.
bal <- tapply(nested[nested$dbh > 15, "ba"], nested[nested$dbh > 15, "plotID"], sum) * expf.large bas <- tapply(nested[nested$dbh <= 15, "ba"], nested[nested$dbh <= 15, "plotID"], sum) * expf.small
Finally, we sum up the BA ha\(^{-1}\) for large and small plots.
ba.ha <- bal + bas ## Error: non-conformable arrays
The error message is printed because there are small plots that do not contain any trees, i.e., bal and bas do not have the same length. Here is a simple workaround.
nested$plotID <- as.factor(nested$plotID) bal <- tapply(nested[nested$dbh > 15, "ba"], nested[nested$dbh > 15, "plotID"], sum) * expf.large bas <- tapply(nested[nested$dbh <= 15, "ba"], nested[nested$dbh <= 15, "plotID"], sum) * expf.small bal[is.na(bal)] <- 0 bas[is.na(bas)] <- 0 ba.ha <- bal + bas
Next, we compute the mean of the BA ha\(^{-1}\) per plot to estimate the population BA ha\(^{-1}\).
(ba.nested.mean <- mean(ba.ha)) ## [1] 34.62
Finally, we construct the confidence intervals around our estimated mean.
ba.nested.se <- sd(ba.ha)/sqrt(n)) ## [1] 3.245 (ba.nested.ser <- sd(ba.ha)/sqrt(n)/mean(ba.ha) * 100) ## [1] 9.376 (conf <- ba.nested.se * qt(0.975, n - 1)) ## [1] 6.522 mean(ba.ha) - conf ## [1] 28.09 mean(ba.ha) + conf ## [1] 41.14
[edit] Additional exercises
Repeat the tasks from the last exercise (Section [sub:fixedex]). Use the data in nested.Ex. Trees with a DBH \(\leq\) 15 cm have only been measured within a smaller circular plot with \(r=10\) meters.
[edit] Related articles
- Previous article: fixed area plots
- Next article: k-tree sampling