Estimating the length of the forest edge

[−] Forest inventory

[+] Introduction to forest inventory

[+] Forest mensuration

[+] Introduction to sampling

[+] Plot design

[+] Sampling design

[+] Estimation issues

[+] Planning issues

[+] UNFCCC Implications for Forest Monitoring

[+] Forest Inventory Examples

  Forest Inventory Glossary

Forest edge length is an important attribute when quantitatively describing the structure of forested landscapes: for a given forest cover, a longer forest edge usually corresponds to a more fragmented landscape. The forest edge length may also used as indicator for forest fragmentation being relevant for both biodiversity monitoring and the sustainable management of large area forest resources. It is also relevant, for example, for research on the function of forests as a sink for atmospheric deposition: atmospheric deposition of both nutrients and pollutants is higher at forest edges, particularly where the forest edges are exposed to the prevailing wind direction.

For research into and modelling of all three classes of edge effects, the determination of edge lengths in a given study region is required. Even if it is some times stated that, with respect to biodiversity aspects and atmospheric depositions the forest edge structure is more important than forest edge length, the lengths of differently structured forest edges are still relevant input for modelling. Forest edge length determination is frequently done manually or by automatic delineation using remote sensing imagery. However, it can also be done by sample based estimation either in remote sensing imagery or from terrestrial sample plots.

Forest edge length is the length of the virtual line that separates forest from non-forest. Just as it is difficult to clearly define “forest”, it is not simple to clearly define the line where forest ends. It is interesting to note that in most remote sensing based studies the delineation of the forest edge is done without explicitly and clearly giving a “measurement protocol”.

Forest edge length is an important input variable to calculate landscape metrics that describe the spatial pattern of forests; in a comprehensive factor analysis, Riijters et al. (1995) demonstrate that edge length is among the most relevant landscape variables for their derivation. Landscape metrics are usually derived from maps; few studies focus on sample based estimation of these metrics (examples are Hunsaker et al. 1994, Kleinn 2000). Rudis (2006) uses sample based forest edge length estimates to characterise forest edge-interior fragmentation. In this article, such sample based estimation approaches for forest edge length are presented. This chapter bases largely on Kleinn and Kändler (2011).

Estimating forest edge length

Based on typical plot designs as used in large area forest inventories, there are various approaches for the estimation of forest edge length. Important in this context is that the spatial resolution of such estimation needs to be considered: the finer the spatial resolution the longer will be the estimated line length. An illustrative example for this intuitive fact is elaborated in Kleinn and Kändler (in review) where forest edge length is estimated from the cluster plot design of the German National Forest Inventory at three different spatial resolutions, resulting in three considerably different results.

There are at least three basic approaches for the estimation of forest edge length differing in the attribute which is observed per plot. They are briefly dealt with in the following sub-chapters.

Mapped plots

Figure 1 Example for mapping forest boundary on circular plots: forest edges are surveyed on 25m radius plots that intersect with the forest boundary. One plot is assumed to contain a maximum of two border lines that are to be measured. If the forest boundary is a straight line within the plot (above), two points on that line at a minimum distance of 10m from each other were surveyed by azimuth and distance from the plot centre so that the position of the line relative to the circular plot could be recovered and the edge length within the plot calculated. If the forest boundary was not a straight line, then the polygon corner was surveyed from the plot centre and one point on each line (below). While corner points of the forest edge polygon may also be surveyed outside the plot area, the length is only calculated for the sections inside the plot (bold lines) (Kleinn and Kändler).

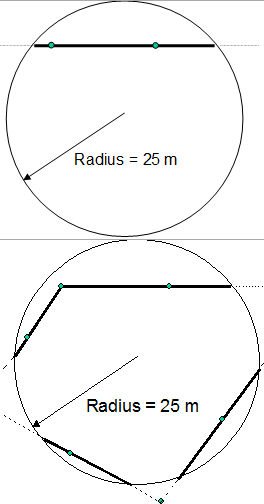
Here, the line length is directly measured on the fixed area plots and estimation follows the usual estimators with plot expansion factors. An example is illustrated in Figure 1 as implemented in the second German National Forest Inventory.

Assuming 25m radius plots, the estimation of forest edge length for an inventory region goes as follows: let \(l_b\) be the observed forest edge length in meters on a 25m radius plot; a per plot estimator of forest edge length per hectare \(l_ha\) results from standard plot expansion by

\[\hat{l}_{ha}=s\frac{10^4}{\pi{r}^2}l_b=\frac{32}{\pi}l_b\,\]

where r = radius of plot [m] = 25m, here.

The factor 2, in addition to the expansion factor, is introduced in that formula because when sampling only forest plots ‑ that is, plots with their centers inside the forest ‑ one evaluates only approximately half of all sample plots that can potentially intersect with the forest boundary: intersecting sample plots with their centers outside forest are not considered, although they would occur on average in about the same number as the intersecting forest plots. Therefore, assuming symmetry, we double the number of intersecting forest plots – accepting a slight underestimation that comes from the fact that for closed polygons with an overall convex shape, one expects on average several more intersecting circular plots with centers outside that polygon.

Averaging over n cluster plots yields the estimated mean forest edge length per hectare \(\hat{L}_{mean}\)

\[\hat{L}_{mean}=\frac{\sum_{i=1}^n(l_{ha})_i}{n}\,\]

where \((l_{ha})_i=0\) for those cluster plots that do not intersect.

The total forest edge length is estimated by expanding to the total area A [ha] as

\[\hat{L}_{tot}=A\frac{\sum_{i=1}^n(l_{ha})_i}{n}\,\]

and the variance of the estimated total forest edge length is estimated by

\[\hat{var}(\hat{L}_{tot})=A^2\frac{\sum_{i=1}^n\left[(l_{ha})_i-\hat{L}_{mean}\right]^2}{n(n-1)}\,\]

Line intersect sampling

The number of intersections of a sample line with the forest edge is determined. There are different possibilities in common forest inventories as to which line feature of a plot design to utilize as sample line:

• in large area forest inventories, frequently clusters of sub-plots are used. Then, the connecting line between the sub-plots can easily be used as sample line;
• in any fixed area plot design, the perimeter of the plot can be used as sample line; then, a border plot intersects with the forest boundary exactly 2 times (only for very large sample plots would more than two intersections be a realistic expectation!).

For the corresponding estimators for line intersect sampling, read the article Line intersect sampling.

Counting the border plots

The longer the forest edge length in a particular region, the higher the proportion of plots that intersect with the forest boundary will be; of course, we are referring here to plots to which a clearly defined shape and size can be attributed. Then, by simply counting the intersecting cluster plots, it is possible to estimate the length of the perimeter line as worked out in Kleinn (2000). The approach varies with the plot shape. Here, the estimator for square plots of side length s is given. Solutions for other plot shapes are given in Kleinn (2000). The estimators for total forest edge length in km \(\hat{L}_{tot}\) and its variance \(\hat{var}(\hat{L}_{tot})\) are

equation 1	\[\hat{L}_{tot}=\frac{\pi}{4}\frac{A}{s}\frac{n_b}{n}=\frac{\pi}{4}\frac{A}{s}p_b\,\]
equation 2	\(\hat{var}(\hat{L}_{tot})=\frac{1}{n-1}\left(\frac{A\pi}{4s}\right)^2\{p_b(1-p_b)\}\,\)

with

\(A\,\)	=	size of the inventory area;
\(s\,\)	=	side length of the square sample plot used;
\(n_b\,\)	=	number of cluster plots that intersect with the forest edge (boundary clusters);
\(n\,\)	=	sample size = total number of clusters in the inventory region;
\(p_b\,\)	=	\(\frac{n_b}{n}\,\)

Note that the only variable in these estimators is \(n_b\), the number of cluster plots that intersect with the forest boundary; all other terms are constant for a given inventory design! And that means, that by simply counting the number of boundary plots an estimation of the forest edge length can be produced (under a number of assumptions, of course).