Simple random sampling examples
(Created page with " Category:Forest Inventory Examples") |
|||
| Line 1: | Line 1: | ||
| + | ====Example 1:==== | ||
| + | |||
| + | <br> | ||
| + | In thissection, SRS estimators are illustrated with an example. This examplewill be pursued through the entire Lecture notes and illustrates thatdifferent sampling designs perform differently for the same populationand with the same sample size. | ||
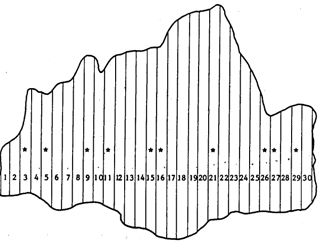
| + | The example population has<math>N = 30</math> individual elements; we may imagine 30strip plots that cover a forest area (Figure 73). This dataset willalso be used in the further chapters for comparison among theperformance of different sampling techniques. | ||
| + | Table 11 liststhe values of the 30 units. Here, for SRS, we are only interested inthe y values. The <math>x</math> values are a measure forthe size (area) of the strips; this will later be used in the contextof other estimators. | ||
| + | From this population we get the following parametric values: | ||
| + | |||
| + | |||
| + | <blockquote><math>\mu= \frac{\sum_{i=1}^N y_i}{N} = 7.0667</math> and<math>\sigma^2 = \frac{\sum_{i=1}^N (y_i - \mu)^2}{N} =7.1289</math></blockquote> | ||
| + | |||
| + | |||
| + | If we take samples of size <math>n=10</math>, then the parametric error variance of the estimated mean is: | ||
| + | |||
| + | |||
| + | <blockquote><math>var (\bar {y}) = \frac {N-n}{N-1} * \frac {\sigma^2}{n} =0.491645</math> </blockquote> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <blockquote>'''Table 1:'''Example Population of N = 30 individual elements</blockquote> | ||
| + | |||
| + | <blockquote> | ||
| + | <div style="float:left"> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !Number | ||
| + | !y | ||
| + | !x | ||
| + | |- | ||
| + | |1 ||2 ||50 | ||
| + | |- | ||
| + | |2 ||3 ||50 | ||
| + | |- | ||
| + | |3 ||6 ||100 | ||
| + | |- | ||
| + | |4 ||5 ||100 | ||
| + | |- | ||
| + | |5 ||6 ||125 | ||
| + | |- | ||
| + | |6 ||8 ||130 | ||
| + | |- | ||
| + | |7 ||6 ||130 | ||
| + | |- | ||
| + | |8 ||7 ||140 | ||
| + | |- | ||
| + | |9 ||8 ||140 | ||
| + | |- | ||
| + | |10 ||6 ||130 | ||
| + | |- | ||
| + | |11 ||7 ||140 | ||
| + | |- | ||
| + | |12 ||7 ||150 | ||
| + | |- | ||
| + | |13 ||9 ||160 | ||
| + | |- | ||
| + | |14 ||8 ||170 | ||
| + | |- | ||
| + | |15 ||10 ||180 | ||
| + | |- | ||
| + | |16 ||9 ||200 | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div style="float:left"> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !Number | ||
| + | !y | ||
| + | !x | ||
| + | |- | ||
| + | |17 ||12 ||210 | ||
| + | |- | ||
| + | |18 ||8 ||210 | ||
| + | |- | ||
| + | |19 ||14 ||210 | ||
| + | |- | ||
| + | |20 ||7 ||200 | ||
| + | |- | ||
| + | |21 ||12 ||200 | ||
| + | |- | ||
| + | |22 ||9 ||180 | ||
| + | |- | ||
| + | |23 ||8 ||160 | ||
| + | |- | ||
| + | |24 ||6 ||140 | ||
| + | |- | ||
| + | |25 ||7 ||120 | ||
| + | |- | ||
| + | |26 ||4 ||90 | ||
| + | |- | ||
| + | |27 ||5 ||90 | ||
| + | |- | ||
| + | |28 ||6 ||100 | ||
| + | |- | ||
| + | |29 ||4 ||100 | ||
| + | |- | ||
| + | |30 ||3 ||80 | ||
| + | |- | ||
| + | |align="left" |'''Mean''' | ||
| + | |'''7.0667''' | ||
| + | |'''13950''' | ||
| + | |- | ||
| + | |align="left" |'''Pop. variance''' | ||
| + | |'''7.1289''' | ||
| + | |'''2087.25''' | ||
| + | |} | ||
| + | </div> | ||
| + | <br> | ||
| + | [[image:SkriptFig_73.jpg|frame|center|Example population]] | ||
| + | </blockquote> | ||
| + | <br style="clear:both" /> | ||
| + | |||
| + | |||
| + | |||
| + | Thisvalue will be compared in the subsequent chapters with the errorvariances produced by other sampling techniques with the same samplesize <math>n=10</math>. The square root of the errorvariance is the standard error; and this is the true parametricstandard error which we strive to estimate from a single sample then.To recap: the parametric standard error is the standard deviation of''all possible samples'' of size <math>n=10</math>. In aconcrete sampling study, we have only one single sample of size<math>n=10</math> and from this sample the standard errorcan only be ''estimated''. | ||
| + | |||
| + | |||
| + | |||
| + | ====Example 2:==== | ||
| + | |||
| + | <br> | ||
| + | Let´stake one single sample of <math>n=10</math> from thepopulation of <math>N=30</math> given in Figure 1 and Table1. Assume that the following elements were randomly selected: | ||
| + | |||
| + | |||
| + | <blockquote> | ||
| + | <div style="float:left; margin-right:2em"> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !Number | ||
| + | !<math>y_i</math> | ||
| + | |- | ||
| + | |3 ||6 | ||
| + | |- | ||
| + | |5 ||6 | ||
| + | |- | ||
| + | |9 ||8 | ||
| + | |- | ||
| + | |11 ||7 | ||
| + | |- | ||
| + | |15 ||10 | ||
| + | |- | ||
| + | |16 ||9 | ||
| + | |- | ||
| + | |21 ||12 | ||
| + | |- | ||
| + | |26 ||4 | ||
| + | |- | ||
| + | |27 ||5 | ||
| + | |- | ||
| + | |29 ||4 | ||
| + | |} | ||
| + | </div> | ||
| + | </blockquote> | ||
| + | |||
| + | Wetake now these ten selected sampling elements to produce estimations ofthe population parameters of interest. The estimated mean, variance inthe population and error variance are, respectively: | ||
| + | <blockquote> | ||
| + | <math>\bar y = \hat {\mu} = 7.1 m^3</math> | ||
| + | <br> | ||
| + | <math>s^2 = \hat \sigma^2 = 6.9889</math> | ||
| + | <br> | ||
| + | <math>v\hat {a}r (\bar y) = 0.4659 = \frac {N-n}{N} * \frac {s^2}{n} = fpc \frac {s^2}{n}</math> | ||
| + | </blockquote> | ||
| + | |||
| + | Observe,that all estimated values differ from the true parametric values. Inpractice, however, we will never come to know how much this deviationactually is because the parametric values remain unknown. | ||
| + | <br> | ||
| + | However,we can make a probabilistic statement about the range in which weexpect the true value to be; which is the confidence interval. For theestimated mean, the confidence interval is calculated from theestimated standard error and an assumption about the distribution ofthe sample means which is reflected in the value of the''t''-distribution. Accepting an error probability of<math>\alpha = 5%</math> that our statement is wrong, thewidth of one side of the confidence interval is: | ||
| + | <blockquote> | ||
| + | <math>t_{\alpha,v}S_{\bary} = 2.262*0.6826 = 1.5440</math> and then <math>P(5.5560< \mu < 8.6440)\,\!</math>. | ||
| + | </blockquote> | ||
| + | |||
| + | |||
| + | Thisreads: the probability that the true parametric mean is in the intervalbetween 5.556 and 8.644 is 0.95; it may however be that the trueparametric mean is smaller or larger; this is the error probability of<math>\alpha = 5%</math>. The given ''t''-value can be readfrom tables or calculated from functions that usually every statisticalsoftware has built in. The actual values are depending on the degreesof freedom and the chosen error probability. | ||
| + | |||
| + | |||
| + | |||
| + | One may also calculate the confidence interval for the estimated variance in the population; which we do not here. | ||
| + | |||
| + | |||
| + | |||
| + | Theabove sample has a size of ''n=10'' and a ''sampling intensity'' of ''f= 10/30*100 = 33%''. Here, sampling intensity can be calculated interms of number of sampling units. Usually, however, the samplingintensity in forest inventories is calculated in terms of | ||
| + | |||
| + | |||
| + | <blockquote><math>f= \frac {total\, area\, of\, all\, sample\, plots}{total\, area\, of\,inventory\, region}</math></blockquote> | ||
| + | |||
| + | |||
| + | '''Estimation of the total:''' The estimator of the total is | ||
| + | <blockquote><math>\hat\tau = N * \bar y</math>, here: <math>\hat \tau = N * \bary = 30 * 7.1 m^3 = 213</math>,</blockquote> | ||
| + | |||
| + | |||
| + | and the estimated variance of the estimated total is | ||
| + | |||
| + | <blockquote><math>\hat{var}(\hat \tau) = N^2\,v{\hat a}r(\bar y) = 30^2 * 0.4659 =419.31</math>.</blockquote> | ||
| + | <br> | ||
| + | |||
| + | |||
[[Category:Forest Inventory Examples]] | [[Category:Forest Inventory Examples]] | ||
Revision as of 14:53, 14 December 2010
Example 1:
In thissection, SRS estimators are illustrated with an example. This examplewill be pursued through the entire Lecture notes and illustrates thatdifferent sampling designs perform differently for the same populationand with the same sample size.
The example population has\(N = 30\) individual elements; we may imagine 30strip plots that cover a forest area (Figure 73). This dataset willalso be used in the further chapters for comparison among theperformance of different sampling techniques.
Table 11 liststhe values of the 30 units. Here, for SRS, we are only interested inthe y values. The \(x\) values are a measure forthe size (area) of the strips; this will later be used in the contextof other estimators.
From this population we get the following parametric values:
\(\mu= \frac{\sum_{i=1}^N y_i}{N} = 7.0667\) and\(\sigma^2 = \frac{\sum_{i=1}^N (y_i - \mu)^2}{N} =7.1289\)
If we take samples of size \(n=10\), then the parametric error variance of the estimated mean is:
\(var (\bar {y}) = \frac {N-n}{N-1} * \frac {\sigma^2}{n} =0.491645\)
Table 1:Example Population of N = 30 individual elements
Number y x 1 2 50 2 3 50 3 6 100 4 5 100 5 6 125 6 8 130 7 6 130 8 7 140 9 8 140 10 6 130 11 7 140 12 7 150 13 9 160 14 8 170 15 10 180 16 9 200
Number y x 17 12 210 18 8 210 19 14 210 20 7 200 21 12 200 22 9 180 23 8 160 24 6 140 25 7 120 26 4 90 27 5 90 28 6 100 29 4 100 30 3 80 Mean 7.0667 13950 Pop. variance 7.1289 2087.25
Thisvalue will be compared in the subsequent chapters with the errorvariances produced by other sampling techniques with the same samplesize \(n=10\). The square root of the errorvariance is the standard error; and this is the true parametricstandard error which we strive to estimate from a single sample then.To recap: the parametric standard error is the standard deviation ofall possible samples of size \(n=10\). In aconcrete sampling study, we have only one single sample of size\(n=10\) and from this sample the standard errorcan only be estimated.
Example 2:
Let´stake one single sample of \(n=10\) from thepopulation of \(N=30\) given in Figure 1 and Table1. Assume that the following elements were randomly selected:
Number \(y_i\) 3 6 5 6 9 8 11 7 15 10 16 9 21 12 26 4 27 5 29 4
Wetake now these ten selected sampling elements to produce estimations ofthe population parameters of interest. The estimated mean, variance inthe population and error variance are, respectively:
\(\bar y = \hat {\mu} = 7.1 m^3\)
\(s^2 = \hat \sigma^2 = 6.9889\)
\(v\hat {a}r (\bar y) = 0.4659 = \frac {N-n}{N} * \frac {s^2}{n} = fpc \frac {s^2}{n}\)
Observe,that all estimated values differ from the true parametric values. Inpractice, however, we will never come to know how much this deviationactually is because the parametric values remain unknown.
However,we can make a probabilistic statement about the range in which weexpect the true value to be; which is the confidence interval. For theestimated mean, the confidence interval is calculated from theestimated standard error and an assumption about the distribution ofthe sample means which is reflected in the value of thet-distribution. Accepting an error probability of\(\alpha = 5%\) that our statement is wrong, thewidth of one side of the confidence interval is:
\(t_{\alpha,v}S_{\bary} = 2.262*0.6826 = 1.5440\) and then \(P(5.5560< \mu < 8.6440)\,\!\).
Thisreads: the probability that the true parametric mean is in the intervalbetween 5.556 and 8.644 is 0.95; it may however be that the trueparametric mean is smaller or larger; this is the error probability of\(\alpha = 5%\). The given t-value can be readfrom tables or calculated from functions that usually every statisticalsoftware has built in. The actual values are depending on the degreesof freedom and the chosen error probability.
One may also calculate the confidence interval for the estimated variance in the population; which we do not here.
Theabove sample has a size of n=10 and a sampling intensity of f= 10/30*100 = 33%. Here, sampling intensity can be calculated interms of number of sampling units. Usually, however, the samplingintensity in forest inventories is calculated in terms of
\(f= \frac {total\, area\, of\, all\, sample\, plots}{total\, area\, of\,inventory\, region}\)
Estimation of the total: The estimator of the total is
\(\hat\tau = N * \bar y\), here\[\hat \tau = N * \bary = 30 * 7.1 m^3 = 213\],
and the estimated variance of the estimated total is
\(\hat{var}(\hat \tau) = N^2\,v{\hat a}r(\bar y) = 30^2 * 0.4659 =419.31\).