Global Positioning System (GPS)

sorry:

This section is still under construction! This article was last modified on 04/14/2011. If you have comments please use the Discussion page or contribute to the article!

This is an Article about the Global Positioning System (GPS) in general. For an introduction to the Garmin GPS receiver see Garmin GPS.

Functional principle

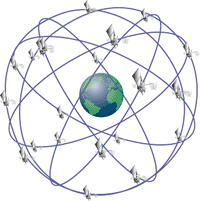
Sattelite navigation systems are used for three-dimensional positioning on the surface of the earth. In contrast to other methods of mensuration or positioning, no fixed points on the earth's surface are used as reference points, but satellites circling in the earth's orbit.

GPS (NAVSTAR-GPS = Navigation System with Satellite Timing and Ranging - Global Positioning System) was the first satellite based navigation system to be established by the pentagon. Main components of this system were 24 satellites (21 satellites plus 3 active backup satellites), encircling the earth on 6 defined tracks in a distance of 20.000 km, allowing positioning on earth's surface in each time and place.

The configuration of GPS satellites in the orbit.

The position of each satellite (so called orbital information) is known at any time and is registered in an earth-bound geocentric coordinate system (WGS84).

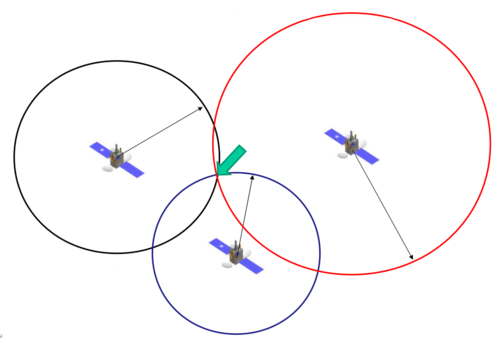
A position on earth's surface can be definitely determined by measuring the distances to three satellites simultaneously. For this task GPS receivers are used, which decode the information sent by the satellite. The functional principle is as follows:

The satellites used to define the current position are equipped with atomic clocks, allowing an extremely precise time measurement. The signals sent by the satellite contain encoded information on the exact moment of transmission. A receiver on earth contains a memory with the coordinates of the orbit of each satellite. This allows for the allocation of a received signal to a specific satellite and the calculation of the runtime (and thus, the distance).

The priciple of GPS positioning with three satellites. The intersection of the three circles defines exactly one point for the receiver to be located. Note that a fourth satellite is needed to graduate a regular measurement error.

Distance measurement

The distance measurement based on the runtime of a electromagnetic satellite-signal can be derived from \[ s = c * t \] with

• s=distance
• c=speed of light
• t=runtime of the signal

The speed of light, in which signals move, is \[c=300.000km/sec = 3*109m/sec\]