Stem volume

sorry:

This section is still under construction! This article was last modified on 02/18/2011. If you have comments please use the Discussion page or contribute to the article!

Forest mensuration lecture notes

[+] Definitions in forest inventory

[+] Functions and models in forest inventory

[+] Measurement devices

[+] Single tree variables

[+] Stand variables

  3D- Terrestrial laser scanning

  Forest Inventory Glossary

General observations

When thinking in terms of timber-production oriented forest management, stem volume is one of the most relevant variables in forest inventory. The volume unit in the metric system is cubic meter (\(m^3\)). Stem volume is one of those variables that can not be measured directly in a forest inventory but that needs to be modeled and predicted from more easily measurable variables. Volume is either determined for the entire stem (total volume) or for defined stem sections (such as commercial volume).

Calculating volume

Direct measurement

The only method of tree volume measurement is by water displacement. However, this is a theoretical approach and not an option in forest inventory…

Volume calculation by section

Figure 1 Subdivision of a stem into sections.

Figure 2 The four basic geometric solids for section-wise volume calculation.

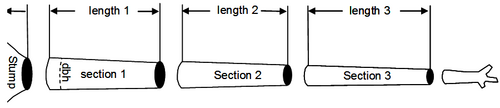
Tree volume determination is always based on measurements of diameter and length. When we do a section-wise volume calculation, the stem is subdivided into sections (Figure 1) of which length \(l\) and basal area \(g\) are measured; basal area is either taken at the middle of the section \(g_m\) or at both the lower end \(g_l\) and the upper end \(g_u\). Then, the following simple formulae are common for section volume calculation:

Huber	\(v=g_ml\,\)
Smalian	\(v=\frac{g_u+g_l}{2}l\,\)
Newton	\(v=\frac{g_u+4g_m+g_l}{6}l\,\)

where the “Huber formula” is simply another name for the volume formula of a cylinder.

All three formulae give the correct result if a section has a quadratic paraboloidal shape or is a cylinder. Newton's formula also applies for a section of a cone. If the section or a log is neither a quadratic paraboloid nor a cylinder, then the Smalian’s or Huber’s formula will produce relatively more errors. For a conoid, i.e. a section of a cone, Smalian's formula overestimates the volume of a section, whereas Huber's formula underestimates the volume by half the amount of the overestimation with Smalian's. The errors given by both formulae are proportional to the length of the log and the square of the difference between the diameters at the two ends. Volumes of logs are normally estimated employing Huber's formula using logs that are as short as is practical.

There are four basic geometric solids with which stem sections can usually be modeled; that is: the cylinder, the apollonic paraboloid, the cone and the neiloid (Figure 2).