Stem shape
The stem shape is characterized by the degree of decreasing diameter with height. Trees may have very different stem shapes where smaller differences can visually usually not be recognized. Depending on the stem shape, the tree volume may be very different for one and the same dbh and the amount of boards and other products that the sawmill can cut from one particular stem does also depend much on the stem shape.
The stem shape can graphically be depicted by the so-called taper curve which gives the radius of the stem at each height, as shown in Figure 1. This requires measurements of diameters at many heights. Therefore, some simpler approaches were developed like the form factor.
Form factor
Stem shape characterization is mainly of interest because, in addition to diameter and length, the stem shape co-determines the stem volume which is one of the most important attributes for timber production oriented forest management. The form factor is a single number that intends to summarize important stem shape information such that this information is useful for volume calculation.
The idea is very simple: one measures a reference diameter (dbh, for example) and tree height; from these two variables the volume of a cylinder can be calculated that is being imagined over the dbh with the tree height as length. Of course, this cylinder has a volume which is much higher than the tree volume. Then, in order to come to the tree volume, we need to introduce a reduction factor, which reduces the cylinder volume (as defined by dbh and height) to the true stem volume. This reduction factor is called form factor \(f\):
\[f=\frac{\mbox{actual stem volume}}{\mbox{volume of a cylinder over the reference diameter}}\,\]
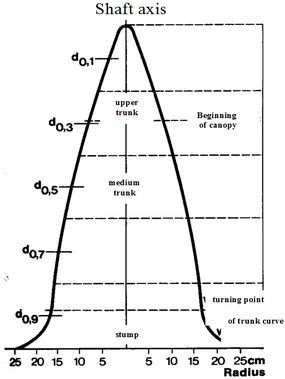
Depending on the reference diameter which is being used to determine the form factor we distinguish the absolute form factor (\({f}_{1.3}\)) and the relative form factor (\({\lambda}_{0.9}\) or \({f}_{0.1}\)), as shown in Figure 2.
- Absolute form factor: dbh is taken as reference diameter, measured at the absolute height of 1.3m. The absolute form factor is usually written as (\(f_{1.3}\)).
- Relative form factor: the diameter at 10% of tree height is taken as a reference to calculate the cylinder volume. The relative form factor is usually written as \(f_{0.1}\), in older text books also as \(\lambda_{0.9}\).
Once the form factor for a species is known (from earlier studies for example), the stem volume can easily be calculated from the simple formula
\[V=ghf\,\]
where
\[g=\mbox{basal area},\,\]
\[h=height\,\]
and
\[f=\mbox{form factor}.\,\]
Actually the form factor can be seen as the simplest volume model, predicting tree volume as a function of dbh, height and form factor. Form factors vary between species, but also with age, site, competition, crown size, etc. They are commonly in the order of magnitude of 0.45-0.55.
Form factors can also be determined for the commercial stem length (instead for the entire tree). This form factor is then, of course, applicable only for volume calculation of that stem section. Only the absolute form factor is being used for commercial height.
Form factors for the commercial stem length are usually in the order of magnitude of \(f_{comm}=0.7\) and can perfectly be used to rapidly calculate the volume of the stem section.