Global Positioning System (GPS)

sorry:

This section is still under construction! This article was last modified on 04/15/2011. If you have comments please use the Discussion page or contribute to the article!

This is an Article about the Global Positioning System (GPS) in general. For an introduction to the Garmin GPS receiver see Garmin GPS.

Functional principle

Sattelite navigation systems are used for three-dimensional positioning on the surface of the earth. In contrast to other methods of mensuration or positioning, no fixed points on the earth's surface are used as reference points, but satellites circling in the earth's orbit.

GPS (NAVSTAR-GPS = Navigation System with Satellite Timing and Ranging - Global Positioning System) was the first satellite based navigation system to be established by the pentagon. Main components of this system were 24 satellites (21 satellites plus 3 active backup satellites), encircling the earth on 6 defined tracks in a distance of 20.000 km, allowing positioning on earth's surface in each time and place .

The configuration of GPS satellites in the orbit.

The position of each satellite (so called orbital information) is known at any time and is registered in an earth-bound geocentric coordinate system (WGS84).

A position on earth's surface can be definitely determined by measuring the distances to three satellites simultaneously. For this task GPS receivers are used, which decode the information sent by the satellite. The functional principle is as follows:

The satellites used to define the current position are equipped with atomic clocks, allowing an extremely precise time measurement. The signals sent by the satellite contain encoded information on the exact moment of transmission. A receiver on earth contains a memory with the coordinates of the orbit of each satellite. This allows for the allocation of a received signal to a specific satellite and the calculation of the runtime (and thus, the distance).

The priciple of GPS positioning with three satellites. The intersection of the three circles defines exactly one point for the receiver to be located. Note that a fourth satellite is needed to graduate a regular measurement error.

Distance measurement

The distance measurement based on the runtime of a electromagnetic satellite-signal can be derived from \[ s = c * t \] with

• s=distance
• c=speed of light
• t=runtime of the signal

The speed of light in which signals move is \[c=300.000km/sec = 3*109m/sec\] The high velocity of the signals makes high demands on distance measurement, as a very precise timing is necessary. If e.g. a distance of 1 m is to be exactly measured, timing must take place on 3,3*10^-9 seconds exactly (=3,3 nanoseconds).

Also, a very precise synchronization of clocks in the system is necessary. For this reason, the satellites are equipped with very short-term stable quartz clocks and very long-term stable atomic clocks. Average GPS receivers only feature quite “cheap” quartz clocks, resulting in a higher measuring error. To decrease this error, a “permanent” distance measurement is conducted. I.e. the distance measurement to the respective satellites takes place over a longer time period. By calculating the mean of all obtained values, the measurement becomes the more precise the longer it is conducted.

The distances measured with the clocks are called pseudoranges. To gain more exact ranges (and thus more exact positions), signals from four satellites are used. The fourth satellite serves to graduate the error of the clocks, thus being a reference for different time measurements.

Accuracy of GPS positionig

It is easy to recognize that the accuracy of positioning depends on many factors:

• The earth is rotating during mensuration
• The satellites are moving (at about 4km/sec.)
• The runtime of signals is influenced by the current state of the atmosphere
• Interference of signals (after previous reflection)
• The signal may be artificially distorted by the provider
• Other sources of error (operating error, software error...)

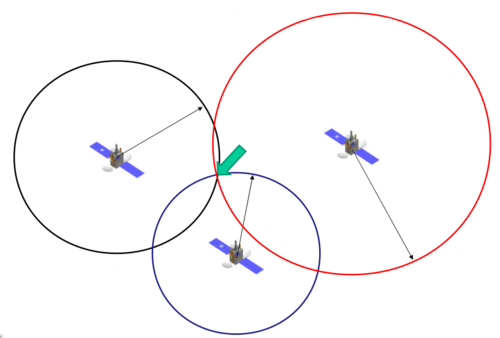
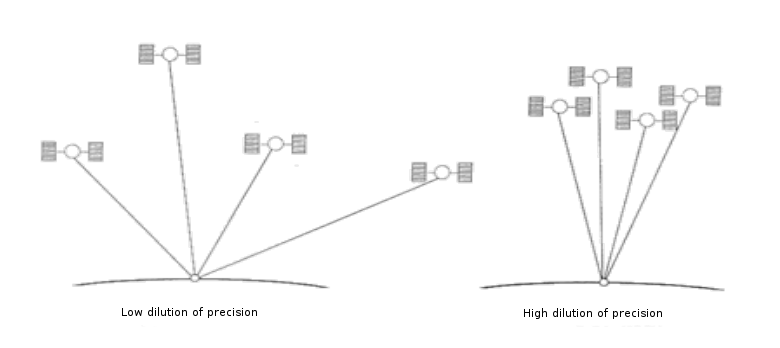
Also, the spatial distribution of the located satellites in the canopy has a significant influence on the accuracy of positioning. Due to geometric reasons positioning is less accurate if satellites are located close to each other. If satellites are located close to the horizon, this can lead to impreciseness due to longer runtimes through the atmosphere and resulting deceleration of the signals (atmospheric reasons). The optimal constellation of satellites is given if one satellite is located in the zenith and the others are standing equally distributed 15° above the horizon.

Interference

If GPS positioning is conducted near to buildings, cars, water surfaces or other reflecting objects, it is possible that the direct signal interferes with reflected signals. If possible, a minimum distance should be maintained (e.g. 10m from cars).

Calculation of precision values: Geometric Dilution of Precision (GDOP)

Dilution of precision is the most common degree for the quantification of precision. It is computed by the software in the receiver based on a compilation of accuracy information.

The dilution of precision (DOP) depending on the position of GPS satellites in the canopy.

Related articles

• Differential Global Positioning System (DGPS)
• Garmin GPS