Stem volume

sorry:

This section is still under construction! This article was last modified on 02/18/2011. If you have comments please use the Discussion page or contribute to the article!

Forest mensuration lecture notes

[+] Definitions in forest inventory

[+] Functions and models in forest inventory

[+] Measurement devices

[+] Single tree variables

[+] Stand variables

  3D- Terrestrial laser scanning

  Forest Inventory Glossary

General observations

When thinking in terms of timber-production oriented forest management, stem volume is one of the most relevant variables in forest inventory. The volume unit in the metric system is cubic meter (\(m^3\)). Stem volume is one of those variables that can not be measured directly in a forest inventory but that needs to be modeled and predicted from more easily measurable variables. Volume is either determined for the entire stem (total volume) or for defined stem sections (such as commercial volume).

Calculating volume

Direct measurement

The only method of tree volume measurement is by water displacement. However, this is a theoretical approach and not an option in forest inventory…

Volume calculation by section

Figure 1 Subdivision of a stem into sections.

Figure 2 The four basic geometric solids for section-wise volume calculation (Kleinn 2007).

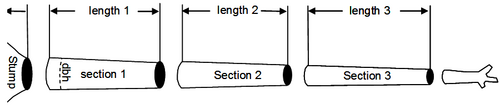
Tree volume determination is always based on measurements of diameter and length. When we do a section-wise volume calculation, the stem is subdivided into sections (Figure 1) of which length \(l\) and basal area \(g\) are measured; basal area is either taken at the middle of the section \(g_m\) or at both the lower end \(g_l\) and the upper end \(g_u\). Then, the following simple formulae are common for section volume calculation:

Huber	\(v=g_ml\,\)
Smalian	\(v=\frac{g_u+g_l}{2}l\,\)
Newton	\(v=\frac{g_u+4g_m+g_l}{6}l\,\)

where the “Huber formula” is simply another name for the volume formula of a cylinder.

All three formulae give the correct result if a section has a quadratic paraboloidal shape or is a cylinder. Newton's formula also applies for a section of a cone. If the section or a log is neither a quadratic paraboloid nor a cylinder, then the Smalian’s or Huber’s formula will produce relatively more errors. For a conoid, i.e. a section of a cone, Smalian's formula overestimates the volume of a section, whereas Huber's formula underestimates the volume by half the amount of the overestimation with Smalian's. The errors given by both formulae are proportional to the length of the log and the square of the difference between the diameters at the two ends. Volumes of logs are normally estimated employing Huber's formula using logs that are as short as is practical.

There are four basic geometric solids with which stem sections can usually be modeled; that is: the cylinder, the apollonic paraboloid, the cone and the neiloid (Figure 2).

The taper curve

Figure 3 Illustration of a taper curve which models the stem shape from the tree bottom (left) to the top (right). The radius is given as a function of tree height/stem length. By rotating this curve, we obtain a solid which is a model for the stem from which the volume can be calculated. (Kleinn 2007).

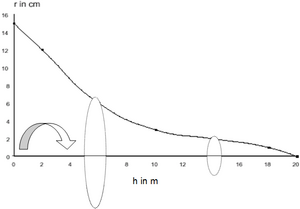
The taper curve gives stem radii or diameters as a function of height. It is assumed that the stem has a perfectly circular shape so that only one side of the curve needs to be determined. Once the taper curve is known mathematically, the stem volume can easily be calculated by a rotation integral of this curve. Of course, this is not only possible for the entire stem, but also for any stem section in which we might be interested. This makes the taper curve a very useful tool, for example for assortment purposes. Figure 3 illustrates the concept of a taper curve.

The complete taper curve goes from the bottom of the stem (usually the felling cut) up to the top of the tree where radius is 0.

When a taper curve is to be determined for a particular tree, a number of diameter measurements have to be taken at different heights. And it is a matter of cost-efficiency to try to define the heights where the diameters are to be measured such that as few as possible measurements need to be taken in order to achieve a defined precision.

1. The most basic way to build a taper “curve“ would be to take a number of measurements and to connect the corresponding values in the graph with straight lines, thus producing a polygon. While this is not a very realistic representation of a real stem because we make the assumption that between two measurement points the diameter decreases linearly with tree height, it is a simple and quick approach and volume calculations can be acceptable if enough measurements had been taken, that is, if the linear sections between the “bending points” are not too long.
   
2. If not too many measurements had been taken one may try to fit a mathematical function that passes through all measured points. Higher order polygons are well suited for this purpose and various authors have proposed other, more complex models (an excellent overview can be found in Rojo et al. 2005).
   
3. The probably most appropriate technique is the splines interpolation.
   For the splines interpolation approach (and that does, in fact, also hold for fitting one single mathematical function) one needs to carefully think how to distribute the radius measurements along the stem. Various important factors are to be considered, among them:

• the generated taper curve should represent the stem realistically and allow volume predictions with the required accuracy; unrealistic irregularities should not occur;
  
• not more than necessary diameter measurements shall be taken, for reasons of cost-efficiency;
  
• diameter measurements shall, above all, be taken (a) where there is the larger part of the tree volume (that is, in the lower part of the stem) and (b) where the changes in curvature are large (and that is also in the very lower part of the stem).
  
• the taper curve shall pass through the lowest point of the stem (felling cut) and through the highest point (tip of the tree) where the diameter is 0 if the entire stem is to be modeled.
  

Empirical simulation studies showed that with 4-6 points (diameter measurements) well distributed along the stem the splines interpolation yields very good results. The recommendation derived in one of those studies (Kleinn 1989) is summarized in Table 1. These measurements are done with the techniques for the measurement of upper diameters as described above. Or they are taken at felled trees wherever these are available (if those are regularly harvested trees, however, it must be taken into account that these trees do possibly not represent the typical taper characteristics of all trees in the stand but only those of the sub-set that was considered due for harvesting!).

Number of measurements	Relative heights of additional d-measurements
4	0.50
5	0.25	0.65
0.20	0.45	0.80