Statistical estimations
| Line 1: | Line 1: | ||
| − | {{improve}} | + | {{improve}}{{Ficontent}} |
| − | {{ | + | |
__TOC__ | __TOC__ | ||
| − | |||
| − | |||
[[File:3.5-fig00.png|right|thumb|300px|'''Figure 1''' The estimator is the calculation algorithm (formula) that produces the estimation (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] | [[File:3.5-fig00.png|right|thumb|300px|'''Figure 1''' The estimator is the calculation algorithm (formula) that produces the estimation (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] | ||
Revision as of 13:10, 26 October 2013
| Attention!: |
This article must be enhanced to meet the AWF-Wiki quality standards! Please visit the Discussion Page of this article for details! |
Contents |
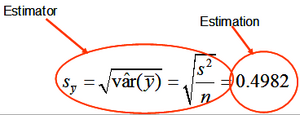
We are interested to know the true population parameters but are not able to determine them. We use, therefore, sampling to produce estimations which we take then as approximations for the true population values; always knowing that estimations carry an error.
Estimations are the principal result of sampling studies. All results of a sample are estimations and must be interpreted as such; they help us to learn something about the unknown parameters of the population of interest.
Notations
There are some conventions in what refers to the notation of population parameters and estimated statistics:
| parametric mean | \(\mu\,\) |
| estimated mean | \(\bar{y}\,\) |
| parametric variance | \(\sigma^2\,\) |
| estimated variance | \(s^2\,\) |
| regression coefficients | \(\beta\,\) |
| estimated coefficients | \(b\,\) |
| unknown population parameter | \(\theta\,\) |
| sample based estimation | \(\hat\theta\,\) |
The “ ^ ” is generally used to make clear that an expression is a sample based estimation. If, for example the variance of variable \(X\) is denoted \(var(X)\), then the estimated variance of \(X\) would be written as \(\hat{var}(X)\). For the estimated mean and the estimated variance, one could also write \(\hat\mu\) and \(\hat\sigma^2\), respectively.
There are various important desirable characteristics of estimators, among them unbiasedness and relative efficiency (when comparing to other estimators); these two are briefly characterized in what follows. It is emphasized here that these are properties of the estimators, not of the estimations!
Unbiasedness
An estimator is unbiased, if it produces on the average estimations that equal the population parameter. Formally: (the expected value of the estimated parameter is equal to the true value of the parameter). If this case is not satisfied, i.e., then the estimator is biased. The bias can be calculated from , but is usually unknown in a particular sampling study.
An empirical interpretation of an unbiased estimator is as follows: if we would take all possible samples from a population following a defined sampling design, then each of these samples would produce one estimation. The mean of all these individual estimations (which is the expected value of the estimation) would finally be equal to the true population parameter. In the case of a biased estimator, we can usually not separate out the bias; that means, what we determine by calculating the error variance is the Mean Square Error that embraces the measure of statistical precision and the bias, resulting in
If , we have an unbiased estimator and obviously the sample variance and the mean square error are identical . What was described in this section is the estimator bias. The term “bias” is sometimes also used in other contexts and should then not be confused with estimator bias: if the selection of sample is not strictly at random but certain types of sampling elements are systematically preferred or excluded, then one speaks some times of selection bias. A selection bias may be present when sample trees are selected for convenience along roads because it may be expected that trees at the forest edge along roads have different characteristics than trees inside the stands. When an observer introduces – for whatever reason – a systematic error into the observations, this is some times called observer bias. This may happen, for example, when damage classes or quality classes are to be assessed that include a certain amount of visual assessment.
Relative efficiency
If, in a sampling study, we have the choice between different sampling designs or within the same sampling design between different estimators, we wish to apply the most efficient one; that is the one that yields best precision for a given effort. This involves the comparison with alternative estimators or/and other sampling designs: If and are two unbiased estimators, relative efficiency is simply calculated as the ratio of the error variances of the two estimators. It should be observed that this is valid for and not necessarily for; that is, from data of a sampling study we can only estimate the relative efficiency.
Point estimates vs. interval estimates
For each statistic that is been estimated (such as a mean, a variance, a correlation coefficient, …) there are two basic types of statistical estimations, the “point estimate”, which estimates the parameter of interest, and the “interval estimate” which estimates the precision of the point estimate.
Standard error (of the mean)
The standard error is a measure of the variability of estimation; it is the square root of the error variance. Error variance and standard error can be estimated for any estimated statistic; here, we refer to the estimated mean.
An empirical illustration of the standard error is: if we take all possible samples (for a defined sampling design) then we will produce many estimated means. These means follow a distribution which has, in the case of an unbiased estimator, a mean value which is equal to the true population mean. The variance of this distribution of means is the error variance of the mean, and the standard error is the standard deviation of the means. This standard error is also called standard error of the mean. The estimated error variance is denoted or as and the standard error as or SE. The standard error of the mean can either be given in absolute or in relative terms; the latter is the ratio of the standard error of the mean and the mean and is frequently denoted as SE%.
For a random sample of size n, the parametric standard error is calculated from and the sample based standard error of the mean is estimated from . This estimator holds for sampling with replacement and for small samples or large populations, that is when only a small portion of the population comes into the sample (5% or less, say). For sampling without replacement, however, we would expect that the standard error is 0 when n = N. But this is obviously not the case for the above estimator: as s is always greater 0, the expression cannot become 0. In order to make sure that this property holds, we must introduce the finite population correction (fpc) into the standard error estimator for sampling without replacement: . Then, for finite populations (or relatively large samples) the estimated standard error is , which obviously becomes 0 if sample size n=N.
If the parametric standard error is to be calculated, the finite population correction is . In order to make the standard error smaller, that is the estimation more precise; one may increase the sample size. In the expression , the sample size appears as square root; that means: if we wish to increase precision by the factor f (that is reduce the standard error by 1/f), we need to multiply the sample size by f²; example: if we wish to reduce the standard error to a half (that is: doubling precision), we must take 4 times as many sample.
Confidence Interval (CI)
For an estimation, the confidence interval defines an upper and lower limit within which the true (population) value is expected to come to lie with a defined probability. This probability is frequently set to 95%, meaning that an error of is accepted (other a are also possible, of course). In order to be able to build such a confidence interval, the distribution of the estimated values need to be known. It is known in sampling statistics, that the estimated mean follows a normal distribution if the sample is large (n>>30, say), and the t distribution with ν degrees of freedom when the sample is small (n<30, say). For a defined value α for the error probability the width of the confidence interval for the estimated mean is given by , where t comes from the t-distribution and depends on sample size (df = degrees of freedom=n-1) and the error probability. Then,
As with the standard error of the mean, the width of the confidence interval (CI) can be given in absolute (in units of the mean value) or in relative terms (in %, relative to the estimated mean).
If an estimation is accompanied by a precision statement, one must clearly say whether that is the standard error or half the width of the confidence interval! For larger sample sizes and α=5%, the t-value is , that is around 2 so that as a rule of thumb we may say that half the width of the confidence interval is given by twice the standard error: . For smaller sample sizes, the t-value will be larger.
References
- ↑ Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.