Volume functions
(→Modeling stem volume) |
|||
| Line 20: | Line 20: | ||
Various groups of volume functions are distinguished. The most simple ones are those that model volume as a function exclusively of ''dbh''; these volume models are some times also referred to as [[volume tariffs]]. They are applied for smaller area [[forest inventory|forest inventories]] like [[stand inventories]]. The fact that neither height nor [[stem shape]] is explicitly included into that model means that we assume that both height and stem shape can be sufficiently well predicted also by ''dbh''. This is approximately true, above all, for the small area forest inventories, where a major field of application for these volume tariffs exists. Table 1 gives some of these tariffs. It should be observed that, although it is only one subject-matter variable that is being included, it is not simple linear regressions as ''dbh'' does also occur as ''dbh²'' which is then a second variable in the model. | Various groups of volume functions are distinguished. The most simple ones are those that model volume as a function exclusively of ''dbh''; these volume models are some times also referred to as [[volume tariffs]]. They are applied for smaller area [[forest inventory|forest inventories]] like [[stand inventories]]. The fact that neither height nor [[stem shape]] is explicitly included into that model means that we assume that both height and stem shape can be sufficiently well predicted also by ''dbh''. This is approximately true, above all, for the small area forest inventories, where a major field of application for these volume tariffs exists. Table 1 gives some of these tariffs. It should be observed that, although it is only one subject-matter variable that is being included, it is not simple linear regressions as ''dbh'' does also occur as ''dbh²'' which is then a second variable in the model. | ||
| + | |||
| + | A further category of volume functions uses ''dbh'' and height as independent (predictor) variables. This adds more flexibility to the model to adjust to changing ''dbh''-height relationships as they occur in medium size forest inventories such as forest enterprise inventories or forest management inventories. This type of volume function assumes that the stem shape can reasonably well be predicted also by ''dbh''. Table 1 gives some of the common models. Interesting there is the model | ||
| + | |||
| + | :<math>v=b_1dbh^2h\,</math> | ||
| + | |||
| + | where volume is calculated as a function of one single “composed” variable: In fact, this function is identical with the form factor approach to volume calculation, only that here the constant values <math>f</math> and <math>\frac{\pi}{4}</math> are together “hidden” in the regression coefficient <math>b_1</math>. | ||
| + | |||
| + | {|border="3" cellpadding="20" cellspacing="0" | ||
| + | |colspan="3"| | ||
| + | '''Table 1''' Different types of models for volume functions, depending on the geographical range of apllication (after Zöhrer 1980<ref name="zöhrer1980">Zöhrer F. 1980. Forstinventur – Ein Leitfaden für Studium und Praxis. Verlag Paul Parey. 207 S.</ref>) | ||
| + | |- | ||
| + | |<math>v=f(dbh)</math> | ||
| + | |<math>v={b_0}+{b_1}{dbh}^2</math> | ||
| + | |Also called volume tarifs | ||
| + | |- | ||
| + | |_ | ||
| + | |<math>v={b_0}+b_1{dbh}+{b_2}{dbh}^2</math> | ||
| + | |Mainly for local studies where homogeneity of site conditions is expected, including relatively strong relationships between ''dbh'' and ''height'' and between ''dbh'' and ''form factor''. | ||
| + | |- | ||
| + | |_ | ||
| + | |_ | ||
| + | |_ | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
==References== | ==References== | ||
Revision as of 21:16, 1 March 2011
| sorry: |
This section is still under construction! This article was last modified on 03/1/2011. If you have comments please use the Discussion page or contribute to the article! |
Contents |
General observations
Volume functions are statistical models that describe the relationship between tree volume (dependent variable, to be predicted) with dbh, some times in combination with other variables such as tree height or an upper stem diameter. Before modeling volume as a function of one or more predictor variables, the variable “volume” needs to be defined. It is frequently defined as total stem volume from the felling cut up to a top diameter of 7 cm or 10 cm. However, volume functions may also refer to commercial volume only which is then the volume of the commercial stem parts which is again a matter of definition. Also, when working in regions with which one is not perfectly familiar, it is a good idea to verify in which height dbh is commonly measured.
Modeling stem volume
Volume functions have very typical shapes. Let’s recall the simple volume model with the form factor that reduces the cylinder volume to the true volume\[V=ghf=\frac{\pi}{4}d^2hf\,\].
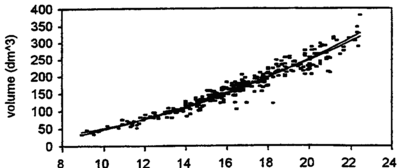
We see that dbh is the only variable that enters squared. That means that dbh has the greatest weight for volume prediction and it means also that, when volume is modeled as a function of dbh, the function must be increasing quadratically. A typical volume function is given in Figure 1. As with height curves, volume functions are given as mathematical functions that can directly be used in analysis software. In earlier times, volume tables were common, where volume could be read as a function of dbh or in a two way table as a function of dbh and height.
Various groups of volume functions are distinguished. The most simple ones are those that model volume as a function exclusively of dbh; these volume models are some times also referred to as volume tariffs. They are applied for smaller area forest inventories like stand inventories. The fact that neither height nor stem shape is explicitly included into that model means that we assume that both height and stem shape can be sufficiently well predicted also by dbh. This is approximately true, above all, for the small area forest inventories, where a major field of application for these volume tariffs exists. Table 1 gives some of these tariffs. It should be observed that, although it is only one subject-matter variable that is being included, it is not simple linear regressions as dbh does also occur as dbh² which is then a second variable in the model.
A further category of volume functions uses dbh and height as independent (predictor) variables. This adds more flexibility to the model to adjust to changing dbh-height relationships as they occur in medium size forest inventories such as forest enterprise inventories or forest management inventories. This type of volume function assumes that the stem shape can reasonably well be predicted also by dbh. Table 1 gives some of the common models. Interesting there is the model
\[v=b_1dbh^2h\,\]
where volume is calculated as a function of one single “composed” variable: In fact, this function is identical with the form factor approach to volume calculation, only that here the constant values \(f\) and \(\frac{\pi}{4}\) are together “hidden” in the regression coefficient \(b_1\).
|
Table 1 Different types of models for volume functions, depending on the geographical range of apllication (after Zöhrer 1980[1]) | ||
| \(v=f(dbh)\) | \(v={b_0}+{b_1}{dbh}^2\) | Also called volume tarifs |
| _ | \(v={b_0}+b_1{dbh}+{b_2}{dbh}^2\) | Mainly for local studies where homogeneity of site conditions is expected, including relatively strong relationships between dbh and height and between dbh and form factor. |
| _ | _ | _ |
References
- ↑ Zöhrer F. 1980. Forstinventur – Ein Leitfaden für Studium und Praxis. Verlag Paul Parey. 207 S.