Sampling with unequal selection probabilities

Revision as of 15:01, 6 January 2011

Introduction

Mostly, one speaks about random sampling with equal selection probabilities: each element of the population has the same probability to be selected. However, there are situations in which this idea of equal selection probabilities does not appear reasonable: if it is known that some elements carry much more information about the target variable, they should also have a greater chance to be selected. Stratification goes into that direction: there, the selection probabilities within the strata were the same, but could be different between strata.

Sampling with unequal selection probabilities is still random sampling, but not simple random sampling, but “random sampling with unequal selection probabilities”. These selection probabilities, of course, must be defined for each and every element of the population before sampling and none of the population elements must have a selection probability of 0.

Various sampling strategies that are important for forest inventory base upon the principle of unequal selection probabilities, including

• angle count sampling (Bitterlich sampling),

• importance sampling,

• 3 P sampling,

• randomized branch sampling.

After a general presentation of the statistical concept and estimators, these applications are addressed.

In unequal probability sampling, we distinguish two different probabilities – which actually are two different points of view on the sampling process:

The selection probability is the probability that element i is selected at one draw (selection step). The Hansen-Hurwitz estimator for sampling with replacement (that is; when the selection probabilities do not change after every draw) bases on this probability. The notation for selection probability is written as \(P_i\) or \(p_i\).

The inclusion probability refers to the probability that element i is eventually (or included) in the sample of size n. The Horvitz-Thompson estimator bases on the inclusion probability and is applicable to sampling with or without replacement. The inclusion probability is generally denoted by \(\pi\).

List sampling = PPS sampling

If sampling with unequal selection probabilities is indicated, the probabilities need to be determined for each element before sampling can start. If a size variable is available, the selection probabilities can be calculated proportional to size. This is then called PPS sampling (probability proportional to size).

Table 1. Listed sampling frame as used for „list sampling” where the selection probability is determined proportional to size. Population element List of the size variables of the population elements List of cumulative sums Assigned range 1 10 10 0 - 10 2 20 30 > 10 - 30 3 30 60 > 30 - 60 4 60 120 > 60 - 120 5 100 220 > 120 - 220

This sampling approach is also called list sampling because the selection can most easily be explained by listing the size variables and select from the cumulative sum with uniformly distributed random numbers (which perfectly simulates the unequal probability selection process). This is illustrated in Table 1: the size variables of the 5 elements are listed (not necessarily any order!) and the cumulative sums calculated. The, uniformly distributed random number is drawn between the lowest and highest possible value of that range, that is from 0 to the total sum. Assume, for example, the random number 111.11 is drawn; this falls into the range “>60 – 120” so that element 4 is selected. Obviously, the elements have then a selection probability proportional to the size variable.

Hansen-Hurwitz estimator

The Hansen-Hurwitz estimator gives the framework for all unequal probability sampling with replacement (Hansen and Hurwitz, 1943). “With replacement” means that the selection probabilities are the same for all draws; if selected elements would not be replaced (put back to the population), the selection probabilities would change after each draw for the remaining elements.

Suppose that a sample of size n is drawn with replacement and that on each draw the probability of selecting the i-th unit of the population is \(p_i\).

Then the Hansen-Hurwitz estimator of the population total is

\[\hat \tau = \frac {1}{n} \sum_{i=1}^n \frac {y_i}{p_i}\]

Here, each observation \(y_i\) is weighted by the inverse of its selection probability \(p_i\).

The parametric variance of the total is

\[var (\hat \tau) = \frac {1}{n} \sum_{i=1}^N p_i \left (\frac {y_i}{p_i} - \tau \right )^2\]

which is unbiasedly estimated from a sample size n from

\[v\hat ar (\hat \tau) = \frac {1}{n} \frac {\sum_{i=1}^n \left (\frac {y_i}{p_i} - \tau \right )^2}{n-1}\]

Hansen-Hurwitz estimator examples: 4 application examples

Horvitz-Thompson estimator

Assuming that with any design, with or without replacement, the probability of including unit i in the sample is \(\pi_i\) (>0), for i=1,2,…, N. The inclusion probability \(\pi_i\) can be calculated from the selection probability \(p_i\) and the corresponding complementary probability (1-p_i), which is the probability that the element is not included into the sample at a particular draw.

After n sample draws, the probability that element i is eventually included into the sample is \(\pi\)=1 - (1-p_i)ⁿ, where (1 - p_i)ⁿ is the probability that the particular element is not included after n draws; the complementary probability to this is then the probability that the element is eventually in the sample (at least selected once).

The Horvitz-Thompson estimator can be applied for sampling with or without replacement, but here it is illustrated for the case with replacement.

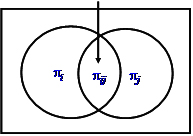
For the variance calculation with the Horvitz-Thompson estimator we also need to know the joint inclusion probability \(\pi_{ij}\) of two elements i and j after n sample draws, that is the probability that both i and j are eventually in the sample, after n draws. This joint inclusion probability is calculated from the two selection probabilities and the two inclusion probabilities after \(\pi_{ij} = \pi_i + \pi_j - \{ 1 - (1 - p_i - p_j)^n \} \) and can be illustrated as in Figure 1.

Figure 1. Diagram illustrating the joint inclusion probability.

The Horvitz-Thompson estimator for the total is \(\hat \tau = \sum_{i=1}^\nu \frac {y_i}{\pi_i}\)

where the sum goes over the \(\nu\) distinc elements (where \(\nu\) is the Greek letter nu) in the sample of size n (and not over all n elements)

The parametric error variance of the total is

\[var(\hat \tau)=\sum_{i=1}^\nu \left (\frac {1 - \pi_i}{\pi_i} \right ) y_i^2 + \sum_{i=1}^N \sum_{j \ne i} \left (\frac {\pi_{ij} - \pi_i \pi_j}{\pi_i \pi_j} \right ) y_i y_j\]

which is estimated by

\[v\hat ar(\hat \tau)=\sum_{i=1}^\nu \left (\frac {1 - \pi_i}{\pi_i^2} \right ) y_i^2 + \sum_{i=1}^N \sum_{j \ne i} \left (\frac {\pi_{ij} - \pi_i \pi_j}{\pi_i \pi_j} \right ) \frac {y_i y_j}{\pi_{ij}}\]

A simpler (but slightly biased) approximation for the estimated error variance of the total is

\[v\hat ar(\hat \tau) = \frac {N - \nu}{N} \frac {1}{\nu} \frac {\sum_{i=1}^\nu (\tau_i -\hat \tau)^2}{\nu - 1}\]

where \(\tau_i\) is the estimation for the total that results from each of the \(\nu\) sample.

{{Exercise message=Horvitz-Thompson estimator examples text=application example }}

Bitterlich sampling

For the inclusion zone approach where for each tree an inclusion zone is defined, see the corresponding article "[Inclusion zone approache]". If used,the inclusion probability is then proportional to the size of this inclusion zone – which actually defines the probability that the correspondent tree is included in a sample.

We saw, for example, that angle count sampling (Bitterlich sampling) selects the trees with a probability proportional to their basal area and we emphasized that this fact makes Bitterlich sampling so efficient for basal area estimation. In contrast, point to tree distance sampling, or k-tree sampling, has inclusion zones that do not depend on any individual tree characteristic but only on the spatial arrangement of the neighboring trees; therefore, point-to tree distance sampling is not particularly precise for any tree characteristic.