Distance based plots
(→Unbiased estimator) |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Ficontent}} |
| − | + | ||
| − | + | ||
[[File:4.5.1-fig63.png|right|thumb|300px|'''Figure 1''' Some variations of ''k''-tree sampling (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] | [[File:4.5.1-fig63.png|right|thumb|300px|'''Figure 1''' Some variations of ''k''-tree sampling (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] | ||
[[File:4.5.1-fig64.png|right|thumb|300px|'''Figure 2''' Illustration why the simple expansion factor approach does produce a systematic overestimation for ''k''-tree sampling (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] | [[File:4.5.1-fig64.png|right|thumb|300px|'''Figure 2''' Illustration why the simple expansion factor approach does produce a systematic overestimation for ''k''-tree sampling (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] | ||
| Line 21: | Line 19: | ||
''k''-tree sampling may also be implemented as a transect of fixed width and variable length (see Figure 1 C) where the transect is being extended until the ''k''-tree is reached. | ''k''-tree sampling may also be implemented as a transect of fixed width and variable length (see Figure 1 C) where the transect is being extended until the ''k''-tree is reached. | ||
| − | We focus here on case A in Figure 1, the unrestricted ''k''-tree distance sampling. A common approach to estimation from fixed area plots is to calculate an [[Fixed_area_plots#The_plot_expansion_factor|expansion factor]] which converts the per-plot values to their equivalent per hectare; to calculate the expansion factor a plot area needs to be defined which obviously depends in some way on the distances between the [[sample point]] and the ''k'' trees. By using a seemingly straightforward approach and defining the plot area as a circle with radius equal to the distance to the ''k'' tree, however, we produce a systematic overestimation, i.e. a positive estimator [[bias]]. | + | We focus here on case A in Figure 1, the unrestricted ''k''-tree distance sampling. A common approach to estimation from [[fixed area plots]] is to calculate an [[Fixed_area_plots#The_plot_expansion_factor|expansion factor]] which converts the per-plot values to their equivalent per hectare; to calculate the expansion factor a plot area needs to be defined which obviously depends in some way on the distances between the [[sample point]] and the ''k'' trees. By using a seemingly straightforward approach and defining the plot area as a circle with radius equal to the distance to the ''k'' tree, however, we produce a systematic overestimation, i.e. a positive estimator [[bias]]. |
Taking the area defined by the distance to the ''k'' tree we are establishing the smallest possible circular plot and this in turn yields the largest possible expansion factor. If we extended the radius up to but not including the ''k''+1 tree, there would still be ''k'' trees within the plot but the expansion factor would be smaller! This is illustrated in Figure 2. | Taking the area defined by the distance to the ''k'' tree we are establishing the smallest possible circular plot and this in turn yields the largest possible expansion factor. If we extended the radius up to but not including the ''k''+1 tree, there would still be ''k'' trees within the plot but the expansion factor would be smaller! This is illustrated in Figure 2. | ||
| Line 28: | Line 26: | ||
<br> | <br> | ||
| − | ==Empirical | + | ==Empirical approximations== |
A number of (biased) empirical estimators have been introduced while a (difficult to apply though) design-unbiased estimator was only presented by Kleinn and Vilcko in 2006. | A number of (biased) empirical estimators have been introduced while a (difficult to apply though) design-unbiased estimator was only presented by Kleinn and Vilcko in 2006. | ||
| Line 42: | Line 40: | ||
and | and | ||
| − | :<math>\frac{N}{ha}=\frac{10000}{{\pi}r_6^2}*5.5 | + | :<math>\frac{N}{ha}=\frac{10000}{{\pi}r_6^2}*5.5\,</math> |
respectively, where <math>r_6</math> is the distance from the sample point to the center of the <math>6^th</math>-nearest tree, and <math>d_6</math> is its [[diameter at breast height]]. Then | respectively, where <math>r_6</math> is the distance from the sample point to the center of the <math>6^th</math>-nearest tree, and <math>d_6</math> is its [[diameter at breast height]]. Then | ||
| Line 58: | Line 56: | ||
or as the mean quadratic mean, which corresponds to the radius of the circle that has average area | or as the mean quadratic mean, which corresponds to the radius of the circle that has average area | ||
| − | :<math>r_{ma}=\sqrt{\frac{1}{2}\left(d_k^2+d_{k+1}^2\right)} | + | :<math>r_{ma}=\sqrt{\frac{1}{2}\left(d_k^2+d_{k+1}^2\right)}\,</math> |
In a comprehensive simulation study carried out by Magnussen et al. (2008<ref name="magnussen2008">Magnussen S, C Kleinn and N Picard. 2008. Two new density estimators for distance sampling. European Journal of Forest Research 127:213-224.</ref>) it showed that this approach performed consistently best in terms of bias and error variance when compared to other empirical estimators. | In a comprehensive simulation study carried out by Magnussen et al. (2008<ref name="magnussen2008">Magnussen S, C Kleinn and N Picard. 2008. Two new density estimators for distance sampling. European Journal of Forest Research 127:213-224.</ref>) it showed that this approach performed consistently best in terms of bias and error variance when compared to other empirical estimators. | ||
| Line 64: | Line 62: | ||
==Unbiased estimator== | ==Unbiased estimator== | ||
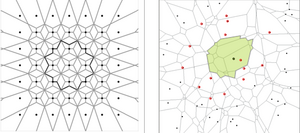
| − | A design-unbiased estimator for ''k''-tree sampling had been developed by finding the inclusion | + | A design-unbiased [[estimator]] for ''k''-tree sampling had been developed by finding the [[inclusion zone]]s (Kleinn and Vilcko 2006<ref name="kleinn_vilcko2006">Kleinn C. and F. Vilčko 2006. Design unbiased estimation for point to tree distance sampling. Canadian Journal of Forest Research 36(6):1407-1414.</ref>) for each one of the ''k'' trees selected in a ''k''-tree sample. These inclusion zones must be such that for any point within that zone the particular tree is either the next or the <math>2^nd</math> next or the <math>3^rd</math> next or … the <math>k^th</math> next tree; they are build as the so-called higher order Voronoi diagrams which require the mapping of a series of trees around the sample trees. While this approach allows developing the first ever unbiased estimator, it is not really practical to map many trees around the sample trees (See also [[Creating_jigsaw_puzzles_in_ArcMap#jigsaw_puzzles_for_k-tree_sampling|jigsaw puzzles for k-tree sampling]]). |
<br> | <br> | ||
Latest revision as of 11:03, 28 October 2013
Point-to-tree distance techniques are also applied in ecological studies in which the k nearest objects (trees or plants) to a sample point are included and constitute the set of sample objects for that particular location. The idea of point-to-tree distance sampling is striking, because it greatly facilitates field work (if the values of k are not too big) under many conditions. Contrary to fixed area plots in which a certain inclusion distance (e.g. the radius of a circular plot up to which trees are included in a sample) is defined, here the number of included trees per sampling location is fixed.
All sample plots contain the same number of k trees, so that both empty plots and very high frequency plots are avoided. Because of the fixed number of trees (objects), this class of response designs is also referred to as fixed-count distance methods while in the context of ecological methodology it is also referred to as plotless methods because there is no need to lay out a fixed plot area.
Here we use the term k-tree sampling to indicate that it is a generalized fixed number of objects that are to be counted. While applications of k-tree sampling can be found in many fields (Engeman et al. 1994, for example, mention density estimation of colonial-nesting seabirds and density of rat damage in sugar cane), we focus here on the forestry context where - in addition to density - many more tree attributes are to be estimated.
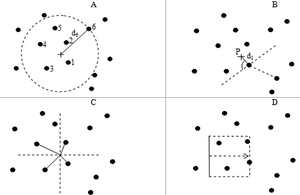
Some variations of k-tree distance sampling are depicted in Figure 1. The 6-tree technique was proposed by Prodan (1968) and is still being used for forest management inventories in South Western Germany. Prodan (1968[3]) and Schöpfer (1969a[4],b[5]) found that a k-value of 6 had optimal properties in terms of practical applicability and statistical performance.
T‑square sampling and the point centered quarter (PCQ) method (Figure 1 B and C) are mainly used in ecological sampling studies and in particular for density estimation; they may be seen as “restricted point-to-tree distance techniques” because they introduce further conditions for the selection of the sample trees, mainly in order to reduce the possibility that among the k selected trees there are pairs of trees very close together: in the T square technique (k=2), the tree closest to the sample point is selected; but then the second tree to be selected is the one closest to the first closest tree on the side opposite to the sample point. It therefore is a combination of point-to-tree and tree-to-tree distance sampling. While T-square sampling is usually presented for k=2, one could extend it to the selection of more trees along the rule defined for the selection of the second tree.
In the PCQ method, four quadrants are established around the sample point and in each quadrant the tree closest to the sample point is selected so that k=4. Variations of this technique include subdividing the space around the sample points into numbers other than j=4 equal sections. Another variation would be to select m > 1 trees in each of the j sectors, forming a k=mj sample.
k-tree sampling may also be implemented as a transect of fixed width and variable length (see Figure 1 C) where the transect is being extended until the k-tree is reached.
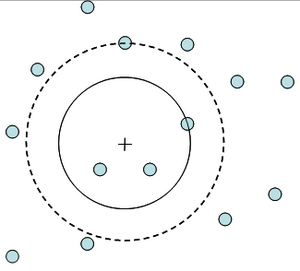
We focus here on case A in Figure 1, the unrestricted k-tree distance sampling. A common approach to estimation from fixed area plots is to calculate an expansion factor which converts the per-plot values to their equivalent per hectare; to calculate the expansion factor a plot area needs to be defined which obviously depends in some way on the distances between the sample point and the k trees. By using a seemingly straightforward approach and defining the plot area as a circle with radius equal to the distance to the k tree, however, we produce a systematic overestimation, i.e. a positive estimator bias.
Taking the area defined by the distance to the k tree we are establishing the smallest possible circular plot and this in turn yields the largest possible expansion factor. If we extended the radius up to but not including the k+1 tree, there would still be k trees within the plot but the expansion factor would be smaller! This is illustrated in Figure 2.
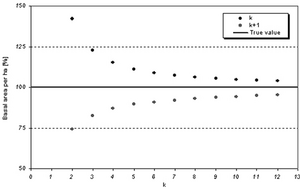
If we follow the expansion factor approach, it is obvious that the correct plot radius must be somewhere between the distance to the k tree and the distance to the k-1 tree. In a simulation study, Kleinn and Vilcko (2006a[6]) showed that the circle plot through the k tree produces a systematic overestimation and the circle plot through the k+1 tree produces a systematic underestimation; where, of course, for increasing values of k the bias becomes smaller and smaller. This is illustrated in Figure 3.
[edit] Empirical approximations
A number of (biased) empirical estimators have been introduced while a (difficult to apply though) design-unbiased estimator was only presented by Kleinn and Vilcko in 2006. The approaches to empirical estimation or approximation can be broken down into two categories:
- empirical approaches in which the appropriate size of a circular plot around the sample point is searched from the distances to the k trees, and
- model-based approaches which are based on assumptions about the point pattern of the trees in the stand.
An early estimator for the 6-tree method uses the idea that the k tree is only half contained in the sample plot, if the radius of the circle plot is measured from the sample point to the center of the k tree (Stoffels 1955 for k=3 and density estimation, Prodan 1968 for k=6 and estimations of any tree attribute). Then, for k=6, the per-plot approximation formula for basal area and number of trees per hectare are
\[\frac{G}{ha}=\frac{10000}{{\pi}r_6^2}\frac{\pi}{4}\left(\sum_{i=1}^{5}d_i^2+\frac{1}{2}d_6^2\right)\,\]
and
\[\frac{N}{ha}=\frac{10000}{{\pi}r_6^2}*5.5\,\]
respectively, where \(r_6\) is the distance from the sample point to the center of the \(6^th\)-nearest tree, and \(d_6\) is its diameter at breast height. Then
\[EF=\frac{10000}{{\pi}r_6^2}\,\]
is the per-plot expansion factor.
For density estimation, Eberhardt (1967[7]) found that the factor (k-1)/k accounted for the positive estimator bias in a random forest and for a particular type of clustering, when the distance to the k tree is used as radius of the sample plot for expansion.
Kleinn and Vilcko (2006[2]) presented another empirical estimator in which the radius of the circular plot is simply calculated from the mean of the distances to the k and to the k+1 tree, either as the arithmetic
\[r_{md}=\frac{1}{2}(d_k+d_{k+1})\,\]
or as the mean quadratic mean, which corresponds to the radius of the circle that has average area
\[r_{ma}=\sqrt{\frac{1}{2}\left(d_k^2+d_{k+1}^2\right)}\,\]
In a comprehensive simulation study carried out by Magnussen et al. (2008[8]) it showed that this approach performed consistently best in terms of bias and error variance when compared to other empirical estimators.
[edit] Unbiased estimator
A design-unbiased estimator for k-tree sampling had been developed by finding the inclusion zones (Kleinn and Vilcko 2006[2]) for each one of the k trees selected in a k-tree sample. These inclusion zones must be such that for any point within that zone the particular tree is either the next or the \(2^nd\) next or the \(3^rd\) next or … the \(k^th\) next tree; they are build as the so-called higher order Voronoi diagrams which require the mapping of a series of trees around the sample trees. While this approach allows developing the first ever unbiased estimator, it is not really practical to map many trees around the sample trees (See also jigsaw puzzles for k-tree sampling).
[edit] References
- ↑ 1.0 1.1 1.2 Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.
- ↑ 2.0 2.1 2.2 Kleinn C. and F. Vilčko 2006. Design unbiased estimation for point to tree distance sampling. Canadian Journal of Forest Research 36(6):1407-1414.
- ↑ Prodan M. 1968. Punktstichprobe für die Forsteinrichtung (A point sample for forest management planning). Forst- und Holzwirt 23(11):225-226.
- ↑ Schöpfer W. 1969a. Die 6-Baum-Stichprobe in der Forsteinrichtung. Teil 1 (6-tree sampling for forest management planning, part 1). Allgemeine Forstzeitung 25:533-536.
- ↑ Schöpfer W. 1969b. Die 6-Baum-Stichprobe in der Forsteinrichtung. Teil 2. (6-tree sampling for forest management planning, part 2) Allgemeine Forstzeitung 26:588-591.
- ↑ Kleinn C. und F Vilčko. 2006a. A new empirical approximation for estimation in k-tree sampling. Forest Ecology and Management 237(2):522-533.
- ↑ Eberhardt LL. 1967. Some developments in distance sampling. Biometrics (23):207-216.
- ↑ Magnussen S, C Kleinn and N Picard. 2008. Two new density estimators for distance sampling. European Journal of Forest Research 127:213-224.