The angle measurement principle
| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Ficontent}} |
| + | [[File:2.2.6-fig13.png|left|285px|thumb|'''Figure 1''' Geometric principle of an optical caliper based on the measurement of an angle. (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] | ||
| − | + | [[:Category:Upper stem diameters|Upper diameters]] can also optically be determined by measuring the small angle that is created when aiming at the left and right hand side of the [[Tree Definition|trunk]], as illustrated in Figure 1. As this angle is very small, extremely accurate angle measurements are necessary to produce useful [[Tree diameter|diameter]] measurements. The horizontal distance to the tree needs also to be determined, where we assume that the tree is perfectly vertical, that is, the upper diameter measured is exactly centered above the [[Diameter at breast height|dbh]]. The basic [[The geometric principle|geometric principle]] is described below. | |
| − | + | ||
| − | [[:Category:Upper stem diameters|Upper diameters]] can also optically be determined by measuring the small angle that is created when aiming at the left and right hand side of the [[Tree | + | |
By measuring the distance to the tree and the slope angle, we can also directly determine at which [[Tree height|height]] our [[Why measuring upper diameters?|upper diameter measurement]] is taken. | By measuring the distance to the tree and the slope angle, we can also directly determine at which [[Tree height|height]] our [[Why measuring upper diameters?|upper diameter measurement]] is taken. | ||
| Line 11: | Line 10: | ||
However, we may safely assume that this underestimation has much less impact on the measurement than the usual measurement errors of angle and distance. From the [[The trigonometric principle|trigonometric relation]] | However, we may safely assume that this underestimation has much less impact on the measurement than the usual measurement errors of angle and distance. From the [[The trigonometric principle|trigonometric relation]] | ||
| − | [[File:2.2.6-fig14.png| | + | [[File:2.2.6-fig14.png|right|285px|thumb|'''Figure 2''' In order to determine the diameter, the angle <math>\beta</math> and the distance <math>e_s</math> need to be determined. (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] |
| − | <math>tan\frac{\beta}{2}=\frac{d/2}{e_s}\,</math> | + | :<math>tan\frac{\beta}{2}=\frac{d/2}{e_s}\,</math> |
the diameter is then determined as | the diameter is then determined as | ||
| − | <math>d=2tan\frac{\beta}{2}e_s\,</math> | + | :<math>d=2tan\frac{\beta}{2}e_s\,</math> |
| + | |||
| + | |||
==References== | ==References== | ||
<references/> | <references/> | ||
| − | |||
{{SEO|keywords=angle measurement,tree diameter,forest inventory,tree measurement,single tree variables | {{SEO|keywords=angle measurement,tree diameter,forest inventory,tree measurement,single tree variables | ||
Latest revision as of 14:13, 27 October 2013
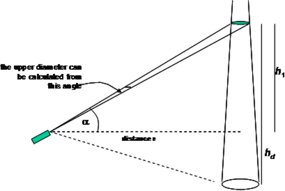
Upper diameters can also optically be determined by measuring the small angle that is created when aiming at the left and right hand side of the trunk, as illustrated in Figure 1. As this angle is very small, extremely accurate angle measurements are necessary to produce useful diameter measurements. The horizontal distance to the tree needs also to be determined, where we assume that the tree is perfectly vertical, that is, the upper diameter measured is exactly centered above the dbh. The basic geometric principle is described below.
By measuring the distance to the tree and the slope angle, we can also directly determine at which height our upper diameter measurement is taken.
From the geometry depicted in Figure 2 we can determine the diameter. Strictly spoken, we are not determining the diameter but the distance between the two points in which the tangents touch the stem. This line does not pass through the center of the tree and we are slightly underestimating the true diameter.
However, we may safely assume that this underestimation has much less impact on the measurement than the usual measurement errors of angle and distance. From the trigonometric relation
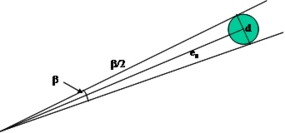
\[tan\frac{\beta}{2}=\frac{d/2}{e_s}\,\]
the diameter is then determined as
\[d=2tan\frac{\beta}{2}e_s\,\]
[edit] References
- ↑ 1.0 1.1 Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.