Pair difference technique example
| (One intermediate revision by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Ficontent}} |
===Example 1=== | ===Example 1=== | ||
| − | Systematic sampling from the example population in Figure 1 (Klein 2007<ref>Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>). | + | [[Systematic sampling]] from the example [[population]] in Figure 1 (Klein 2007<ref>Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>). |
[[File:5.6-fig93.png|right|thumb|300px|'''Figure 1''' Example population of 30 unequally sized strip plots; here, the ratio estimator may be apllied for estimation using plot size as covariable(de Vries 1986<ref>de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. Springer. 399 p.</ref>)]] | [[File:5.6-fig93.png|right|thumb|300px|'''Figure 1''' Example population of 30 unequally sized strip plots; here, the ratio estimator may be apllied for estimation using plot size as covariable(de Vries 1986<ref>de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. Springer. 399 p.</ref>)]] | ||
| Line 14: | Line 14: | ||
As these three samples are the entire population of all possible samples of size 10 taken systematically (that is: equidistantly from the population listing) we can calculate here the expected value of the applied estimators directly. | As these three samples are the entire population of all possible samples of size 10 taken systematically (that is: equidistantly from the population listing) we can calculate here the expected value of the applied estimators directly. | ||
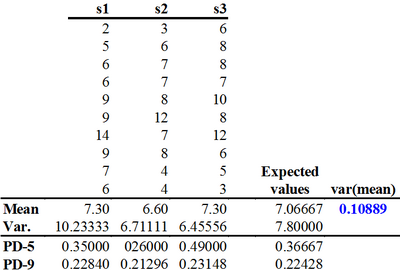
| − | In Table 1, the estimators of simple random sampling were applied to the three samples producing the estimations of the mean and variance. We see that the expected value of the estimated mean is equal to the population value so that we can assume that that estimator is unbiased. However, the expected value of the estimated variance is higher than the true population variance which indicates in an empirical manner that the simple random sampling variance estimator is biased for systematic sampling. | + | In Table 1, the estimators of [[simple random sampling]] were applied to the three samples producing the estimations of the mean and variance. We see that the [[expected value]] of the estimated mean is equal to the population value so that we can assume that that estimator is unbiased. However, the expected value of the estimated variance is higher than the true population variance which indicates in an empirical manner that the simple random sampling variance estimator is biased for systematic sampling. |
The parametric error variance can be calculated as the variance from the population of all estimated means. In this case | The parametric error variance can be calculated as the variance from the population of all estimated means. In this case | ||
| − | <math>var(\bar y)=0.10889\,</math> | + | <math>var(\bar y)=0.10889\,</math> |
which is only about one fifth of the error variance for simple random sampling with the same sample size! If we estimated the error variance of the estimated mean with the simple random sampling estimator we would produce, as expected, a considerable over-estimation (conservative estimation): | which is only about one fifth of the error variance for simple random sampling with the same sample size! If we estimated the error variance of the estimated mean with the simple random sampling estimator we would produce, as expected, a considerable over-estimation (conservative estimation): | ||
| − | <math>var(\bar y)=\frac{7.8}{10}=0.78\,</math> | + | <math>var(\bar y)=\frac{7.8}{10}=0.78\,</math> |
Application of the pair differences technique has also been calculated for each of the three systematic samples. The estimations are given in the last two lines in Table 1. | Application of the pair differences technique has also been calculated for each of the three systematic samples. The estimations are given in the last two lines in Table 1. | ||
Latest revision as of 13:03, 26 October 2013
[edit] Example 1
Systematic sampling from the example population in Figure 1 (Klein 2007[1]).
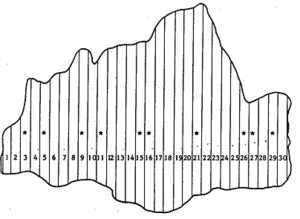
Taking a systematic sample of \(n=10\) elements, there are not many possibilities in our small example population. In fact, if the there shall be an equal distance between the elements in the list, this distance must be \(30/10=3\). Then, there are only three possible systematic samples having element 1, 2, or 3 as starting elements and then taking every third element. These three samples are listed and analyzed in Table 1.
As these three samples are the entire population of all possible samples of size 10 taken systematically (that is: equidistantly from the population listing) we can calculate here the expected value of the applied estimators directly.
In Table 1, the estimators of simple random sampling were applied to the three samples producing the estimations of the mean and variance. We see that the expected value of the estimated mean is equal to the population value so that we can assume that that estimator is unbiased. However, the expected value of the estimated variance is higher than the true population variance which indicates in an empirical manner that the simple random sampling variance estimator is biased for systematic sampling.
The parametric error variance can be calculated as the variance from the population of all estimated means. In this case
\(var(\bar y)=0.10889\,\)
which is only about one fifth of the error variance for simple random sampling with the same sample size! If we estimated the error variance of the estimated mean with the simple random sampling estimator we would produce, as expected, a considerable over-estimation (conservative estimation)\[var(\bar y)=\frac{7.8}{10}=0.78\,\]
Application of the pair differences technique has also been calculated for each of the three systematic samples. The estimations are given in the last two lines in Table 1.
Two options were applied:
- With 5 non-overlapping pairs of observations and
- With 9 overlapping pairs;
where the pairs had been built from neighboring values in the population list.
[edit] References
- ↑ Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.
- ↑ de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. Springer. 399 p.