Statistical estimations

From AWF-Wiki
(Difference between revisions)
Jump to: navigation, search
 
(8 intermediate revisions by 2 users not shown)
Line 1: Line 1:
−
{{improve}}{{Ficontent}}                     
+
{{Ficontent}}                     
−
__TOC__
+
−
 
+
 
[[File:3.5-fig00.png|right|thumb|300px|'''Figure 1''' The estimator is the calculation algorithm (formula) that produces the estimation (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007.  Lecture Notes  for the Teaching Module Forest Inventory. Department of  Forest  Inventory and Remote Sensing. Faculty of Forest Science and  Forest  Ecology, Georg-August-Universität Göttingen. 164  S.</ref>).]]
 
[[File:3.5-fig00.png|right|thumb|300px|'''Figure 1''' The estimator is the calculation algorithm (formula) that produces the estimation (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007.  Lecture Notes  for the Teaching Module Forest Inventory. Department of  Forest  Inventory and Remote Sensing. Faculty of Forest Science and  Forest  Ecology, Georg-August-Universität Göttingen. 164  S.</ref>).]]
 
We are interested to know the true [[population]] parameters but are not able to determine them. We use, therefore, [[:Category:Sampling design|sampling]] to produce estimations which we take then as approximations for the true population values; always knowing that estimations carry an error.
 
We are interested to know the true [[population]] parameters but are not able to determine them. We use, therefore, [[:Category:Sampling design|sampling]] to produce estimations which we take then as approximations for the true population values; always knowing that estimations carry an error.
Line 40: Line 38:
 
The “ ^ ” is generally used to make clear that an expression is a sample based estimation. If, for example the variance of variable <math>X</math> is denoted <math>var(X)</math>, then the estimated variance of <math>X</math> would be written as <math>\hat{var}(X)</math>. For the estimated mean and the estimated variance, one could also write <math>\hat\mu</math> and <math>\hat\sigma^2</math>, respectively.
 
The “ ^ ” is generally used to make clear that an expression is a sample based estimation. If, for example the variance of variable <math>X</math> is denoted <math>var(X)</math>, then the estimated variance of <math>X</math> would be written as <math>\hat{var}(X)</math>. For the estimated mean and the estimated variance, one could also write <math>\hat\mu</math> and <math>\hat\sigma^2</math>, respectively.
  
−
There are various important desirable characteristics of ''estimators'', among them unbiasedness and relative efficiency (when comparing to other estimators); these two are briefly characterized in what follows. It is emphasized here that these are properties of the estimators, not of the estimations!
+
There are various important desirable characteristics of ''estimators'', among them [[Bias|unbiasedness]] and [[relative efficiency]] (when comparing to other estimators). It is emphasized here that these are properties of the estimators, not of the estimations!   
−
+
−
==Relative efficiency==
+
−
 
+
−
If, in a sampling study, we have the choice between different [[:category:sampling design|sampling designs]] or within the same sampling design between different estimators, we wish to apply the most efficient one; that is the one that yields best [[accuracy and precision|precision]] for a given effort. This involves the comparison with alternative estimators or/and other sampling designs:
+
−
 
+
−
If <math>\hat\theta_1</math> and <math>\hat\theta_2</math> are two unbiased estimators, relative efficiency is simply calculated as the ratio of the error variances of the two estimators.
+
−
 
+
−
:<math>RE=\frac{V(\hat\theta_1)}{V(\hat\theta_2)}</math>
+
−
 
+
−
It should be observed that this is valid for <math>var(\hat\theta)</math> and not necessarily for <math>\hat var(\hat\theta)</math>; that is, from data of a sampling study we can only estimate the relative efficiency.  
+
  
 
==Point estimates vs. interval estimates==
 
==Point estimates vs. interval estimates==
  
−
For each statistic that is been estimated (such as a mean, a variance, a correlation coefficient, …) there are two basic types of statistical estimations, the “point estimate”, which estimates the parameter of interest, and the “interval estimate” which estimates the precision of the point estimate.
+
For each statistic that is been estimated (such as a mean, a variance, a correlation coefficient, …) there are two basic types of statistical estimations, the “point estimate”, which estimates the parameter of interest, and the “interval estimate” which estimates the precision of the point estimate. The [[standard error]] is a measure of the variability of estimation and defines the [[confidence interval]] of an estimate.
−
==Standard error (of the mean)==
+
−
 
+
−
The standard error is a measure of the variability of estimation; it is the square root of the error variance.
+
−
Error variance and standard error can be estimated for any estimated statistic; here, we refer to the estimated mean. 
+
−
 
+
−
An empirical illustration of the standard error is: if we take all possible samples (for a defined sampling design) then we will produce many estimated means. These means follow a distribution which has, in the case of an unbiased estimator, a mean value which is equal to the true population mean. The variance of this distribution of means is the error variance of the mean, and the standard error is the standard deviation of the means. This standard error is also called standard error of the mean. The estimated error variance is denoted  or as  and the standard error as  or SE.
+
−
The standard error of the mean can either be given in absolute or in relative terms; the latter is the ratio of the standard error of the mean and the mean and is frequently denoted as SE%. 
+
−
 
+
−
For a random sample of size n, the parametric standard error is calculated from  and the sample based standard error of the mean is estimated from . This estimator holds for sampling with replacement and for small samples or large populations, that is when only a small portion of the population comes into the sample (5% or less, say). For sampling without replacement, however, we would expect that the standard error is 0 when n = N. But this is obviously not the case for the above estimator: as s is always greater 0, the expression  cannot become 0. In order to make sure that this property holds, we must introduce the finite population correction (fpc) into the standard error estimator for sampling without replacement:
+
−
. Then, for finite populations (or relatively large samples) the estimated standard error is , which obviously becomes 0 if sample size n=N. 
+
−
 
+
−
If the parametric standard error is to be calculated, the finite population correction is .
+
−
In order to make the standard error smaller, that is the estimation more precise; one may increase the sample size. In the expression , the sample size appears as square root; that means: if we wish to increase precision by the factor f (that is reduce the standard error by 1/f), we need to multiply the sample size by f²; example: if we wish to reduce the standard error to a half (that is: doubling precision), we must take 4 times as many sample. 
+
−
 
+
−
==Confidence Interval (CI)==
+
−
 
+
−
For an estimation, the confidence interval defines an upper and lower limit within which the true (population) value is expected to come to lie with a defined probability. This probability is frequently set to 95%, meaning that an error of is accepted (other a are also possible, of course). In order to be able to build such a confidence interval, the distribution of the estimated values need to be known. It is known in sampling statistics, that the estimated mean follows a normal distribution if the sample is large (n>>30, say), and the t distribution with ν degrees of freedom when the sample is small (n<30, say).
+
−
For a defined value α for the error probability the width of the confidence interval for the estimated mean is given by , where t comes from the t-distribution and depends on sample size (df = degrees of freedom=n-1) and the error probability. Then,
+
−
 
+
−
As with the standard error of the mean, the width of the confidence interval (CI) can be given in absolute (in units of the mean value) or in relative terms (in %, relative to the estimated mean). 
+
−
 
+
−
If an estimation is accompanied by a precision statement, one must clearly say whether that is the standard error or half the width of the confidence interval!
+
−
For larger sample sizes and α=5%, the t-value is , that is around 2 so that as a rule of thumb we may say that half the width of the confidence interval is given by twice the standard error: . For smaller sample sizes, the t-value will be larger.
+
  
 
==References==
 
==References==

Latest revision as of 09:59, 28 October 2013

Forest inventory
Introduction to forest inventory
Forest mensuration
Introduction to sampling
Plot design
Sampling design
Estimation issues
Planning issues
UNFCCC Implications for Forest Monitoring
Forest Inventory Examples
  Forest Inventory Glossary
Figure 1 The estimator is the calculation algorithm (formula) that produces the estimation (Kleinn 2007[1]).

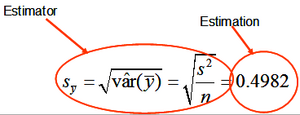
We are interested to know the true population parameters but are not able to determine them. We use, therefore, sampling to produce estimations which we take then as approximations for the true population values; always knowing that estimations carry an error.

Estimations are the principal result of sampling studies. All results of a sample are estimations and must be interpreted as such; they help us to learn something about the unknown parameters of the population of interest.

[edit] Notations

There are some conventions in what refers to the notation of population parameters and estimated statistics:

parametric mean \(\mu\,\)
estimated mean \(\bar{y}\,\)
parametric variance \(\sigma^2\,\)
estimated variance \(s^2\,\)
regression coefficients \(\beta\,\)
estimated coefficients \(b\,\)
unknown population parameter \(\theta\,\)
sample based estimation \(\hat\theta\,\)

The “ ^ ” is generally used to make clear that an expression is a sample based estimation. If, for example the variance of variable \(X\) is denoted \(var(X)\), then the estimated variance of \(X\) would be written as \(\hat{var}(X)\). For the estimated mean and the estimated variance, one could also write \(\hat\mu\) and \(\hat\sigma^2\), respectively.

There are various important desirable characteristics of estimators, among them unbiasedness and relative efficiency (when comparing to other estimators). It is emphasized here that these are properties of the estimators, not of the estimations!

[edit] Point estimates vs. interval estimates

For each statistic that is been estimated (such as a mean, a variance, a correlation coefficient, …) there are two basic types of statistical estimations, the “point estimate”, which estimates the parameter of interest, and the “interval estimate” which estimates the precision of the point estimate. The standard error is a measure of the variability of estimation and defines the confidence interval of an estimate.

[edit] References

  1. ↑ Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.

Retrieved from "http://wiki.awf.forst.uni-goettingen.de/wiki/index.php?title=Statistical_estimations&oldid=9895"
Personal tools
Namespaces

Variants
Actions
Navigation
Development
Toolbox
Print/export