The geometric principle
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Ficontent}} |
| − | + | The geometric principle of measuring [[Tree height|tree height]] is based on the basic principle of similar triangles (intercept theorem). Figure 1 illustrates the geometric principle with the Christen height meter. The device is a simple ruler on which a defined length is marked. A pole is to be put as reference length vertically next to the [[Tree Definition|tree]]. The height scale on the height meter, of course, depends on the length of the pole that is being used. The scaling on the [[Christen height meter]] is made for a four meter pole. One goes now away from the tree until the entire tree is covered by the upper and lower marks (b and c in Figure 1) on the device. The height of the tree can now be read where the top of the pole is being seen on the ruler. This is easily derived by the principle of similar triangles: | |
| − | The geometric principle of measuring [[Tree height|tree height]] is based on the basic principle of similar triangles (intercept theorem). Figure 1 illustrates the geometric principle with the Christen height meter. The device is a simple ruler on which a defined length is marked. A pole is to be put as reference length vertically next to the [[Tree | + | |
:<math>\frac{\bar{bc}}{BC}=\frac{\bar{bd}}{BD}\,</math> | :<math>\frac{\bar{bc}}{BC}=\frac{\bar{bd}}{BD}\,</math> | ||
| Line 11: | Line 10: | ||
and hence | and hence | ||
| − | :<math>h=l\frac{h'}{l'}\,</math> | + | :<math>h=l\frac{h'}{l'}\,</math> |
where <math>h</math> is the total height of the tree, <math>l</math> is the (known) length of the pole, <math>h’</math> is the height value as obtained from the instrument (this is the known fixed length between the ruler’s marks), <math>l’</math> is the height value of the pole as read on the instrument. | where <math>h</math> is the total height of the tree, <math>l</math> is the (known) length of the pole, <math>h’</math> is the height value as obtained from the instrument (this is the known fixed length between the ruler’s marks), <math>l’</math> is the height value of the pole as read on the instrument. | ||
| − | [[File:2.3.4-fig20.png|right|thumb | + | [[File:2.3.4-fig20.png|right|285px|thumb|'''Figure 1''' Height meter of Christen which utilizes the geo-metric principle of height measurements. (Kleinn 2007<ref name="kleinn2007">Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.</ref>).]] |
| − | We must find a point from which the tree top and bottom both can be seen; in various situations in stands with dense [[canopies]], this can be difficult or even impossible. The fact that one can not flexibly change the distance from the tree makes the geometric principle problematic for standard application. | + | We must find a point from which the [[tree top]] and bottom both can be seen; in various situations in stands with dense [[canopies]], this can be difficult or even impossible. The fact that one can not flexibly change the distance from the tree makes the geometric principle problematic for standard application. |
| − | Another very practical instrument for the measurement of tree height along the geometric principle is Kramer´s dendrometer. There the value of | + | Another very practical instrument for the measurement of tree height along the geometric principle is [[Dendrometer|Kramer´s dendrometer]]. There the value of <math>h'</math> on the device is much shorter than on the Christen height meter so that one needs to go even farther away from the tree to be measured. |
| − | When measuring height, certain characteristics of a forest stand have to be taken into account. It is essential that the viewer must be able to view the tree top, otherwise, an overestimation of tree height can occur. Differences in crown structure of softwood and hardwood can contribute to the difficulty of measuring heights. It is usually easier to measure height with softwood because of triangular shape of the crown where the tip of the tree can easily be seen. This is not the case with hardwood since hardwood crowns are more rounded. When the density of a forest stand is high, some trees are oblique so that it is hard to see the tree top. Thus, a certain estimation of where the tree tip is has to be done. | + | When measuring height, certain characteristics of a [[Forest Definition|forest stand]] have to be taken into account. It is essential that the viewer must be able to view the tree top, otherwise, an overestimation of tree height can occur. Differences in [[Crown attributes|crown]] structure of [[softwood]] and [[hardwood]] can contribute to the difficulty of measuring heights. It is usually easier to measure height with softwood because of triangular shape of the crown where the tip of the tree can easily be seen. This is not the case with hardwood since hardwood crowns are more rounded. When the density of a forest stand is high, some trees are oblique so that it is hard to see the tree top. Thus, a certain estimation of where the tree tip is has to be done. |
==References== | ==References== | ||
Latest revision as of 12:58, 27 October 2013
The geometric principle of measuring tree height is based on the basic principle of similar triangles (intercept theorem). Figure 1 illustrates the geometric principle with the Christen height meter. The device is a simple ruler on which a defined length is marked. A pole is to be put as reference length vertically next to the tree. The height scale on the height meter, of course, depends on the length of the pole that is being used. The scaling on the Christen height meter is made for a four meter pole. One goes now away from the tree until the entire tree is covered by the upper and lower marks (b and c in Figure 1) on the device. The height of the tree can now be read where the top of the pole is being seen on the ruler. This is easily derived by the principle of similar triangles:
\[\frac{\bar{bc}}{BC}=\frac{\bar{bd}}{BD}\,\]
in Figure 1 or, in more general terms:
\[\frac{h}{l}=\frac{h'}{l'}\,\]
and hence
\[h=l\frac{h'}{l'}\,\]
where \(h\) is the total height of the tree, \(l\) is the (known) length of the pole, \(h’\) is the height value as obtained from the instrument (this is the known fixed length between the ruler’s marks), \(l’\) is the height value of the pole as read on the instrument.
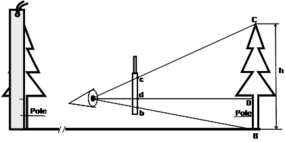
We must find a point from which the tree top and bottom both can be seen; in various situations in stands with dense canopies, this can be difficult or even impossible. The fact that one can not flexibly change the distance from the tree makes the geometric principle problematic for standard application.
Another very practical instrument for the measurement of tree height along the geometric principle is Kramer´s dendrometer. There the value of \(h'\) on the device is much shorter than on the Christen height meter so that one needs to go even farther away from the tree to be measured.
When measuring height, certain characteristics of a forest stand have to be taken into account. It is essential that the viewer must be able to view the tree top, otherwise, an overestimation of tree height can occur. Differences in crown structure of softwood and hardwood can contribute to the difficulty of measuring heights. It is usually easier to measure height with softwood because of triangular shape of the crown where the tip of the tree can easily be seen. This is not the case with hardwood since hardwood crowns are more rounded. When the density of a forest stand is high, some trees are oblique so that it is hard to see the tree top. Thus, a certain estimation of where the tree tip is has to be done.
[edit] References
- ↑ Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.