Haralick Texture
| Line 1: | Line 1: | ||
| − | |||
| − | |||
Image texture is a quantification of the spatial variation of grey tone values. Haralick | Image texture is a quantification of the spatial variation of grey tone values. Haralick | ||
et al. (1973) presented texture measures that may be derived by comparing the values | et al. (1973) presented texture measures that may be derived by comparing the values | ||
| Line 15: | Line 13: | ||
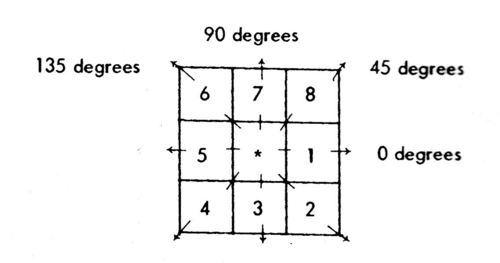
[[File:Texture.png|center|500px|thumb|3x3 window definition and spatial relationship for calculating Haralick texture measures. Pixel 1 and 5 are 0° (horizontal) nearest neighbors to the center pixel * ; pixel 2 and 6 are 135° nearest neighbors; pixels 3 and 7 are 90° nearest neighbors, pixel 4 and 8 are 45° nearest neighbors to the center pixel * (Haralick et al. 1973)]] | [[File:Texture.png|center|500px|thumb|3x3 window definition and spatial relationship for calculating Haralick texture measures. Pixel 1 and 5 are 0° (horizontal) nearest neighbors to the center pixel * ; pixel 2 and 6 are 135° nearest neighbors; pixels 3 and 7 are 90° nearest neighbors, pixel 4 and 8 are 45° nearest neighbors to the center pixel * (Haralick et al. 1973)]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[category:Spatial filtering]] | [[category:Spatial filtering]] | ||
Revision as of 10:59, 17 September 2014
Image texture is a quantification of the spatial variation of grey tone values. Haralick et al. (1973) presented texture measures that may be derived by comparing the values of the digital numbers within a window. An essential component of the concept of the Haralick texture measures is the definition of eight nearest-neighbor resolution cells (Fig.). Now we may define different matrices for different angles (0°,45°,90°,135°) and distances between the horizontal neighboring pixels. Many studies in land cover and forest type classification utilize textural features to improve the classification accuracies. We use the ASTER satellite band number 1 (green) and an inter-pixel sampling distance of one. At first we need to linearly transform the 16-bit ASTER data to 8-bit radiometric resolution.