Resource assessment exercises: nested fixed area plots
(Created page with "{{construction}} In the last subsection we saw that we “measured” 2,158 DBHs on the <math>n=50</math> fixed area plots. Many of the trees are relatively small, i.e., have...") |
|||
| Line 1: | Line 1: | ||
{{construction}} | {{construction}} | ||
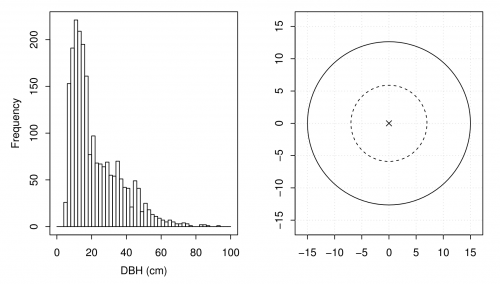
| − | In the last subsection we saw that we “measured” 2,158 DBHs on the <math>n=50</math> fixed area plots. Many of the trees are relatively small, i.e., have small DBHs. Figure | + | In the last subsection we saw that we “measured” 2,158 DBHs on the <math>n=50</math> fixed area plots. Many of the trees are relatively small, i.e., have small DBHs. Figure '''A''' shows a histogram of the variable <code>dbh</code>. The bin width is two centimeters. |
| + | |||
| + | <pre> | ||
| + | bins <- seq(from=0, to=100, by=2) # define bin wiedth (here, 2 cm classes) | ||
| + | hist(fixed.area$dbh, breaks=bins, main="", xlab="DBH (cm)") | ||
| + | </pre> | ||
| + | |||
| + | {{info|message=What the function <code>seq()</code> does|text=The function <code>seq(from, to, by)</code> creates a sequence of values. The argument <code>by</code> defines the step length. Alternatively you can use, e.g., <code>length.out</code>. For example <code>seq(0, 1, length.out = 10)} creates a sequence from zero to one of length 10.\par</code>}} | ||
| + | |||
| + | |||
| + | [[image:Resource assessment hist and nested plot.png|thumb|center|500px|'''Figure A:''' Histogram of DBH in <code>fixed.area</code> and nested sample plot]] | ||
| + | |||
We use the <code>quantile()</code> function to obtain a numerical representation of the DBH distribution. | We use the <code>quantile()</code> function to obtain a numerical representation of the DBH distribution. | ||
| − | <pre>## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% | + | <pre> |
| − | ## 6 9 11 13 15 17 22 28 35 45 93</pre> | + | quantile(fixed.area$dbh, probs=seq(from=0, to=1, by=0.1)) |
| + | |||
| + | ## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% | ||
| + | ## 6 9 11 13 15 17 22 28 35 45 93 | ||
| + | </pre> | ||
| + | |||
| + | {{info|message=What the function <code>quantile()</code> does|text=The function <code>quantile(x, )</code> provides sample quantiles for given probabilities (argument <code>probs</code>). The probabilities have lie between zero and one, i.e., [0, 1].}} | ||
| + | |||
| + | |||
We see that many trees have a DBH below 15 cm. Measuring all the DBHs on a plot is often a tedious task. Moreover, small trees contribute relatively little to the BA ha<math>^{-1}</math>. Can we reduce the number of small trees we need to measure? | We see that many trees have a DBH below 15 cm. Measuring all the DBHs on a plot is often a tedious task. Moreover, small trees contribute relatively little to the BA ha<math>^{-1}</math>. Can we reduce the number of small trees we need to measure? | ||
Revision as of 13:04, 23 July 2014
| sorry: |
This section is still under construction! This article was last modified on 07/23/2014. If you have comments please use the Discussion page or contribute to the article! |
In the last subsection we saw that we “measured” 2,158 DBHs on the \(n=50\) fixed area plots. Many of the trees are relatively small, i.e., have small DBHs. Figure A shows a histogram of the variable dbh. The bin width is two centimeters.
bins <- seq(from=0, to=100, by=2) # define bin wiedth (here, 2 cm classes) hist(fixed.area$dbh, breaks=bins, main="", xlab="DBH (cm)")
 What the function
What the function seq()does- The function
seq(from, to, by)creates a sequence of values. The argumentbydefines the step length. Alternatively you can use, e.g.,length.out. For exampleseq(0, 1, length.out = 10)} creates a sequence from zero to one of length 10.\par
We use the quantile() function to obtain a numerical representation of the DBH distribution.
quantile(fixed.area$dbh, probs=seq(from=0, to=1, by=0.1)) ## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ## 6 9 11 13 15 17 22 28 35 45 93
 What the function
What the function quantile()does- The function
quantile(x, )provides sample quantiles for given probabilities (argumentprobs). The probabilities have lie between zero and one, i.e., [0, 1].
We see that many trees have a DBH below 15 cm. Measuring all the DBHs on a plot is often a tedious task. Moreover, small trees contribute relatively little to the BA ha\(^{-1}\). Can we reduce the number of small trees we need to measure?
In forest inventories nested plots are frequently used (see Figure [fig:hist]). Within the larger area (solid line) all trees with a DBH larger than 15 centimeters are measured, and small trees (\(\leq\)15 cm) are only recorded within the smaller circle (dashed line). The radius of the smaller plot is \(r_{\text{small}}=7.73\) and for the larger we still use a radius of \(r_{\text{large}}=15.45\).
We file MES.RData contains a data.frame named nested. The locations of the plots are exactly the same as for the fixed.area plots. However, we used a threshold diameter for small trees (\(\leq\)15 cm) in a nested plot design.
Here are the number of trees we measured.
## [1] 1624
## [1] 2158
Using the nested plot design we reduced the number of measured DBHs by 534. Does it reduce the precision of the BA ha\(^{-1}\) estimate considerably?
Firstly, we need to calculate the BA for each tree again. Secondly, we need to calculate the expansion factors for the larger and smaller nested plot.
## [1] 15.45
## [1] 7.725
## [1] 187.5
Thirdly, the BA per hectare and plot is calculated for the large and small plots and multiplied with the respective expansion factor.
Finally, we sum up the BA ha\(^{-1}\) for large and small plots.
'
The error message is printed because there are small plots that do not contain any trees, i.e., bal and bas do not have the same length. Here is a simple workaround.
Next, we compute the mean of the BA ha\(^{-1}\) per plot to estimate the population BA ha\(^{-1}\).
## [1] 34.62
Finally, we construct the confidence intervals around our estimated mean.
## [1] 3.245
## [1] 9.376
## [1] 6.522
## [1] 28.09
## [1] 41.14
Exercises
Repeat the tasks from the last exercise (Section [sub:fixedex]). Use the data in nested.Ex. Trees with a DBH \(\leq\) 15 cm have only been measured within a smaller circular plot with \(r=10\) meters.