File list
This special page shows all uploaded files. When filtered by user, only files where that user uploaded the most recent version of the file are shown.
| Name | Thumbnail | Size | User | Description | Versions | |
|---|---|---|---|---|---|---|
| 20:13, 10 December 2010 | 5.4-fig85.png (file) |  | 446 KB | Aspange | 1 | |
| 22:34, 10 December 2010 | 5.4-fig86.png (file) |  | 87 KB | Aspange | 1 | |
| 18:17, 16 December 2010 | 5.2.6-fig74.png (file) |  | 98 KB | Aspange | 1 | |
| 18:59, 16 December 2010 | 5.1.3-fig73.png (file) |  | 78 KB | Aspange | 1 | |
| 20:15, 16 December 2010 | 5.3.4-fig81.png (file) |  | 19 KB | Aspange | (Cluster plot design as used in a regional forest inventory in the NOrthern Zone of Costa Rica (Kleinn 1993). This design is used to illustrate approaches to area estimation.) | 1 |
| 11:08, 22 December 2010 | 5.5.1-fig87.png (file) | 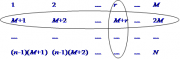 | 58 KB | Aspange | (Illustration of systematic sampling in terms of stratified sampling or cluster sampling. The population of <math>N</math> elements is arranged here in groups of <math>M</math>. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inv) | 1 |
| 11:33, 22 December 2010 | 5.5.2-fig88.png (file) |  | 278 KB | Aspange | (One and the same grid randomly laid over the same area results in different numbers of sample points inside the forest area. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Se) | 1 |
| 11:50, 22 December 2010 | 5.5.3-fig89.png (file) | 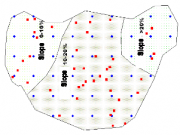 | 68 KB | Aspange | (When a population is sub-divided into strata, systematic sampling always produces proportional allocation of plots. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Fa) | 1 |
| 12:07, 22 December 2010 | 5.5.5-fig90.png (file) |  | 314 KB | Aspange | (Two examples of the difference between random and fixed orientation grids. Left: squares of different side lengths (abscissa) are sampled with grid of unit size. Right: a forest map is sampled with random and fixed orientation grids of different width whe) | 1 |
| 12:12, 23 December 2010 | 5.5.6.4-fig91.png (file) |  | 139 KB | Aspange | (Building pairs of neighboring observations for the approximation of error variance in systematic sampling. Pairs can either be built “exclusively” (below) or overlapping (above). Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module For) | 1 |
| 13:08, 23 December 2010 | 5.5.8-fig92.png (file) | 86 KB | Aspange | (Different patterns of systematic sample grids. A being a square grid, B being a rectangular grid with <math>a:b=2:1</math>, C being a rectangular grid with <math>a:b=8:1</math>, and D being a triangular grid as defined in Matérn (1960). Reference: Mat�) | 1 | |
| 13:14, 23 December 2010 | 5.6-fig93.png (file) | 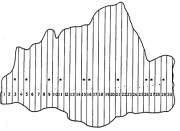 | 118 KB | Aspange | (Example population of 30 unequally sized strip plots; here, the ratio estimator may be apllied for estimation using plot size as covariable (de Vries 1986) Reference: de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. S) | 1 |
| 13:36, 23 December 2010 | 5.5.6.4-tab19.png (file) | 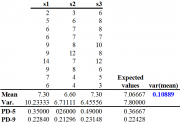 | 923 KB | Aspange | (The population of all possible systematic samples of size <math>n=10</math> drawn from the example population. There are only 3 possibilities. PD-5 and 9 are the estimated error variances from the pair differences method with 5 non-overlapping and 9 overl) | 2 |
| 19:37, 29 December 2010 | 5.6.1-fig93.png (file) | 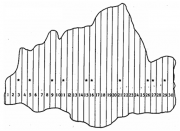 | 687 KB | Aspange | (Example of a population of 30 unequally sized strip plots; here, the ratio estimator may be applied for estimation using plot size as co-variable (DeVries 1986). Reference: de Vries 1986<ref>de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A ) | 1 |
| 23:42, 29 December 2010 | 5.2.6-fig75.png (file) | 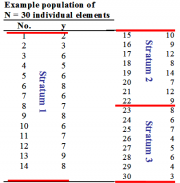 | 490 KB | Aspange | (Sub-dividing the example population (arbitrarily) in three strata, for illustration purposes. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Scienc) | 8 |
| 14:18, 18 January 2011 | 2.1.3.5-tab1.png (file) | 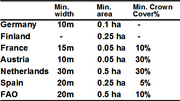 | 438 KB | Aspange | (Comparison of three quantitative criteria of forest definitions as used in some European countries NFI (EC 1996).) | 1 |
| 14:22, 18 January 2011 | 2.1.3.5-fig3.png (file) | 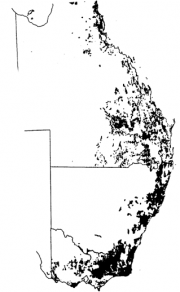 | 485 KB | Aspange | (Forest cover map of Eastern Australia (Bureau of Rural Resources 1991). At the boundary between the two provinces a marked change of the spatial arrangement of forest patches can be observed.) | 1 |
| 14:28, 18 January 2011 | 2.1.3.5-fig4.png (file) | 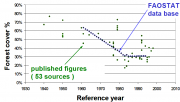 | 1.09 MB | Aspange | (Comparing published forest cover figures for Costa Rica from different sources (Kleinn and Morales 2002).) | 1 |
| 14:59, 18 January 2011 | 2.1.3.6-fig5.png (file) |  | 896 KB | Aspange | (Subdivision of a region into equal size cells for forest cover estimation. Reference: Kleinn C. 2000. Estimating metrics of forest spatial pattern from large area forest inventory cluster samples. Forest Science 46(4):548-557.) | 1 |
| 15:02, 18 January 2011 | 2.1.3.6-fig6.png (file) |  | 1.5 MB | Aspange | (Subdivision of a region into equal size cells for forest cover estimation. Reference: Kleinn C. 2000. Estimating metrics of forest spatial pattern from large area forest inventory cluster samples. Forest Science 46(4):548-557.) | 1 |
| 15:20, 18 January 2011 | 2.1.3.6-tab2.png (file) | 650 KB | Aspange | (Relationship between minimum crown cover percent, reference skill size and forest cover estimates. Reference: Kleinn C. 2000. Estimating metrics of forest spatial pattern from large area forest inventory cluster samples. Forest Science 46(4):548-557.) | 1 | |
| 15:23, 18 January 2011 | 2.1.3.6-fig7.png (file) | 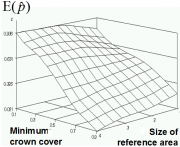 | 549 KB | Aspange | (Graphical illustration of the data presented in table 1. Reference: Kleinn C. 2000. Estimating metrics of forest spatial pattern from large area forest inventory cluster samples. Forest Science 46(4):548-557.) | 1 |
| 16:40, 8 February 2011 | 2.1.4-fig8.png (file) | 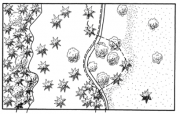 | 105 KB | Aspange | (Some definitions of forest boundary Reference: Kenneweg, H. 2002. Neue methodische Ansätze zur Fernerkundung in den Bereichen Landschaft, Wald und räumliche Planung. In: Dech S et al. (Hrsg.): Tagungsband 19. GFD-Nutzerseminar, 15.-16. Okt. 2002, S. ) | 1 |
| 17:55, 8 February 2011 | 2.2.2-fig9.png (file) | 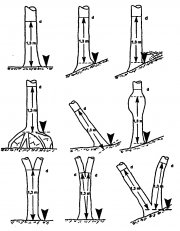 | 967 KB | Aspange | (Illustration of an instruction for dbh measurements. This example is taken from the field manual of the second national forest inventory in Germany. Reference: BMELV. 2007. Survey Instructions for the 2nd National Forest Inventory (2001-2002). Reprint F) | 1 |
| 18:23, 8 February 2011 | 2.2.3.1-fig10.png (file) | 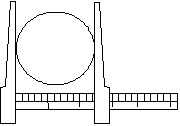 | 23 KB | Aspange | (Principle of ''dbh'' measurement with a caliper Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universit�) | 1 |
| 18:59, 8 February 2011 | 2.2.3.2-tab3.png (file) | 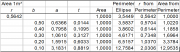 | 734 KB | Aspange | (Illustration of the effect of assuming a perfect circular cross section when determining basal area and dbh by tape-measurements. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remo) | 1 |
| 19:14, 8 February 2011 | Diameter tape.png (file) |  | 1.66 MB | Aspange | (Example für a diameter tape. Reference: treecaresupplies.com) | 1 |
| 17:51, 17 February 2011 | 2.2.5.2-fig11.png (file) | 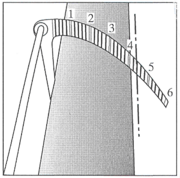 | 157 KB | Aspange | (The Finn caliper: fixed on a pole the tree diameter can be read up to a height of 7m. Reference: Keller M. (ed.). 2005. Schweizerisches Landesforstinventar. Anleitung für die Feldaufnahmen der Erhebung 2004-2007.) | 2 |
| 18:08, 17 February 2011 | 2.2.5.3-fig12.png (file) | 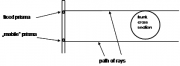 | 64 KB | Aspange | (Measurement rinciple of an optical caliper like Wheeler's pentaprism. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, G) | 1 |
| 18:33, 17 February 2011 | 2.2.6-fig13.png (file) | 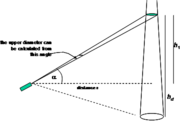 | 111 KB | Aspange | (Geometric principle of an optical caliper based on the measurement of an angle. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest ) | 1 |
| 18:36, 17 February 2011 | 2.2.6-fig14.png (file) | 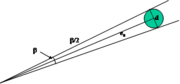 | 54 KB | Aspange | (In order to determine the diameter, the angle <math>\beta</math> and the distance <math>e_s</math> need to be determined. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensi) | 1 |
| 18:51, 17 February 2011 | 2.2.7-fig15.png (file) | 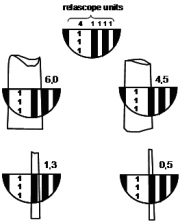 | 85 KB | Aspange | (Relascope units in the mirror relascope. The units are on a micro scale which adjusts automatically to slope; that is, the scale becomes more and more narrower with increasing deviation from the horizontal. By that construction principle it is guaranteed ) | 1 |
| 19:54, 17 February 2011 | 2.3.4-fig20.png (file) | 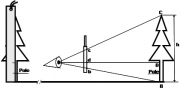 | 87 KB | Aspange | (Height meter of Christen which utilizes the geo-metric principle of height measurements. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science an) | 2 |
| 20:58, 17 February 2011 | 2.5-fig21.png (file) |  | 1.19 MB | Aspange | (Uneven oblique plane as used in Field Manual 2nd Swiss NFI. Reference: Brändli UB, A Herold, H Stierlin und J Zinggeler. 1994. Schweizerisches Landesforstinventar. Anleitung für die Feldaufnahmen der Erhebung 1993-1995. Birmensdorf, Eidg. Forschungsan) | 2 |
| 21:31, 17 February 2011 | 2.6.3-fig23.png (file) | 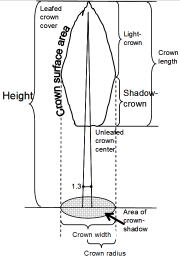 | 1.2 MB | Aspange | (Illustration of some crown attributes. Reference: Kramer, H. and Akca, A. 1995. Leitfaden zur Waldmesslehre. 3rd Edition. J.D. Sauerländers Verlag, Frankfurt. 266p.) | 1 |
| 21:34, 17 February 2011 | 2.6.3-fig24.png (file) | 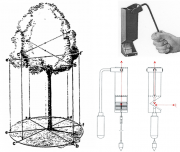 | 1.17 MB | Aspange | (''Left:'' Projection of a tree crown. ''Right:'' Crown mirror - Device to measure tree crown projection. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of F) | 1 |
| 21:51, 17 February 2011 | 2.6.4-fig25.png (file) | 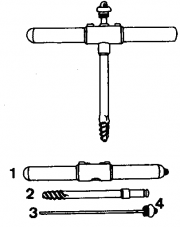 | 204 KB | Aspange | (Increment borer. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.) | 1 |
| 15:37, 18 February 2011 | 2.6.6-fig26.png (file) | 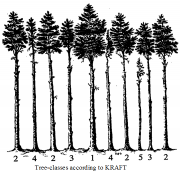 | 820 KB | Aspange | (''1'' predominant ''2'' dominant ''3'' co-dominant ''4'' dominated ''5'' falling behind (according to Kraft)) | 1 |
| 16:09, 18 February 2011 | 2.6.7.2-fig27.png (file) | 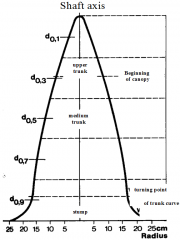 | 993 KB | Aspange | (Example of a taper curve characterizing the shape of a stem.) | 1 |
| 16:25, 18 February 2011 | 2.6.7.2-fig28.png (file) | 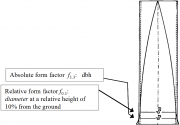 | 1.55 MB | Aspange | (Absolute ans relative form factor measurment.) | 1 |
| 17:20, 18 February 2011 | 2.7.2.2-fig29.png (file) | 513 KB | Aspange | (Subdivision of a stem into sections.) | 1 | |
| 17:25, 18 February 2011 | 2.7.2.2-fig30.png (file) | 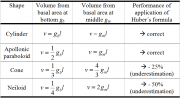 | 1.15 MB | Aspange | (The four basic geometric solids for sectionwise volume calculation. Reference: Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Geor) | 1 |
| 17:36, 18 February 2011 | 2.7.2.3-fig31.png (file) | 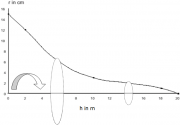 | 773 KB | Aspange | (Illustration of a taper curve which models the stem shape from the tree bottom (left) to the top (right). The radius is given as a function of tree height/stem length. By rotating this curve, we obtain a solid which is a model for the stem from which the ) | 1 |
| 17:52, 18 February 2011 | 2.7.2.3-tab4.png (file) | 373 KB | Aspange | („Optimal“ distribution of measurement points along a stem to determine stem volume with highest precision by interpolation with cubic splines. Three measurement points are “fixed”: at 0.2 m height (assumed felling height), at 1.3 m (dbh) and total) | 1 | |
| 18:26, 18 February 2011 | 2.8.2-fig32.png (file) | 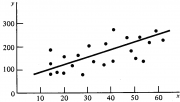 | 474 KB | Aspange | (Straight line representing a linear regression model between variable ''X'' and ''Y''.) | 1 |
| 18:41, 18 February 2011 | 2.8.2-fig33.png (file) | 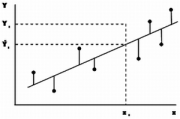 | 175 KB | Aspange | (Illustration of the least squares technique. The distance which is squared is not the perpendicular one but the distance in <math>y</math>-direction as we are interested in predictions over given values of <math>x</math>.) | 2 |
| 19:07, 18 February 2011 | 2.8.3-fig34.png (file) | 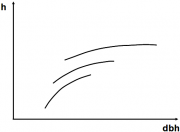 | 568 KB | Aspange | (Height curves in even aged stands exhibit typical changes over time which are depicted here simplified and schematically: they get flatter, shift right on the dbh axis and up on the height axis and cover a wider range of diameters (“become longer”).) | 1 |
| 19:08, 18 February 2011 | 2.8.3-fig35.png (file) | 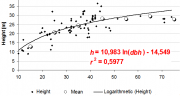 | 825 KB | Aspange | (Simple linear regression with ln(dbh) as sole independent variable. In addition to the data points, the mean heights per 10cm dbh-class are given. In this case, the model is obviously not flexible enough to adjust well to the height values for very large ) | 1 |
| 19:14, 18 February 2011 | 2.8.3-fig36.png (file) | 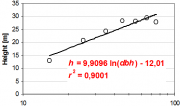 | 480 KB | Aspange | (The same height curve as in Figure 2 but drawn in a grid with ln(''dbh'') on the abscissa instead of ''dbh'' only.) | 1 |
| 20:23, 18 February 2011 | 2.8.3-fig37.png (file) | 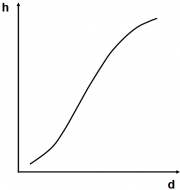 | 774 KB | Aspange | (A typical height curve in a natural uneven-aged stand. If the forest is in a “steady state”, This curve does not change over time and can simultaneously be interpreted as growth curve. Reference: Prodan M., R. Peters, F. Cox and P. Real. 1997.Mensur) | 1 |
 First page |
 Previous page |
 Next page |
 Last page |