Fixed area plots

Fixed area sample plots can have various different shapes including circular, square, rectangular and strip. As to which shape is chosen depends on practical and statistical issues. In terms of practical criteria it is mainly the cost which is of interest and which translates into criteria such as terrain conditions and expected frequency of border trees. Border trees cost time because it needs to be carefully checked whether they are in or not and that implies usually additional distance measurements which are not required for the other trees.
From a practical point of view a circular plots is most rapidly installed wherever the visibility in the stand is good. In a tropical forest with dense understory, it is much easier to establish a strip plot where the field crew walks along the central line and measures all trees up to a defined distance to the right and to the left. A circular plot, however, has the lowest expected number of border trees, because, for a given area, the circle is the geometric shape that has the shortest perimeter.
Coming back to the considerations on spatial autocorrelation, a long rectangular plot (strip plot) covers more different site conditions and is likely to capture more variability per plot. Thus, we may expect higher precision when using strip plots if we compare it with circular plots with the same plot area.
In what refers to the plot size, for a given sampling intensity it is statistically more precise to establish many small plots than few large plots. However, with many small plots, again the cost will be much higher; the decision on Sample size is again a compromise between practical (cost) criteria and statistical (precision). If there is some information on number of stems per hectare, one can calculate, as a rule of thumb, the plot area such that there are on average about 15-20 trees in a sample plot. Typical plot areas are 200 m², 500 m², 1000 m² - but anything is possible. In general sample plots (or any other plot design could be installed as permanent or temporary plot. Especially in context of the estimation on changes this could have a huge influence on precision.
All trees that have the center of their base inside the plot area are sample trees and are being measured. If a tree is a border tree and it is not obvious whether it is in or out, a measurement must help with that decision. If the tree is exactly on the borderline, then one may count one tree and the next such tree not; but actually, when measuring distances with high accuracy, the case that a tree is exactly on the borderline should be very rare. It is only the center point of the tree base that defines whether a tree is in or out. If center point is in but the tree leans completely outside the plot, this is still an in-tree. If the center is not in the plot, but the entire tree leans into the plot, this tree is not observed.
If a defined sample plot is overlapping the forest boundary or the boundary of a stratum, edge correction needs to be applied in order to derive unbiased estimates.
Contents |
The inclusion zone concept
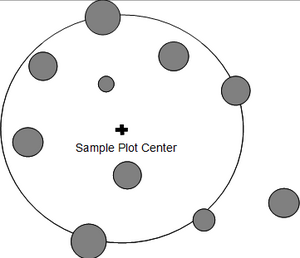
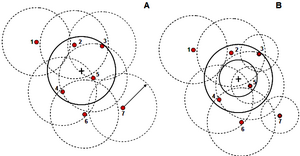
We introduced circular fixed area plots such that a sample point is selected and then all trees within a fixed distance (the plot radius r) are taken as sample trees (see Figure 1). While this plot perspective is intuitively clear and understandable, it does not allow to say anything about the per tree inclusion probability. This however, may be an important component of statistical information.
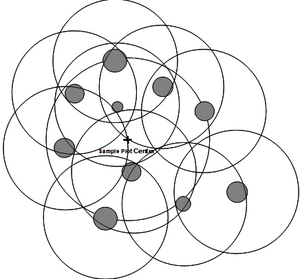
We may change the perspective from the plot perspective to the tree perspective. In that approach, we build a so-called inclusion zone around each tree. The inclusion zone is a measure for the inclusion probability of that particular tree: if a sample point falls into that inclusion zone, then this particular tree is included in a sample. While this sounds maybe complicated, it is extremely helpful in understanding forest inventory sampling and also in deriving unbiased estimators for any plot design.
In the case of fixed area circular plots, the inclusion zone that is centered about each tree has the size and shape of the plot, that is circular. All trees, therefore, have the same selection probability. We now imagine the inclusion zones around all trees and select a sample point. Then, all those trees are selected as sample trees for which the sample point falls into their inclusion zone (Figure 2). Of course, at the end, exactly the same trees are selected as with the first approach (of laying out the sample plot), but in this second approach we take the selection probability explicitly into account.
The inclusion zone concept can be applied also to the other plot designs that are being presented in the rest of this chapter.
The plot expansion factor
In forest inventory, we are usually interested in estimates of the total and in estimates per hectare. The immediate per-plot results are not of major interest. In order to get the estimates per hectare one needs to expand the per-plot observation. This is done with a plot expansion factor. It is important to consider that area related variables refer to the horizontal map plane and a slope correction is necessary in sloped terrain. For fixed area plots, this expansion factor from the per-plot to the per-hectare estimate is calculated from
\[EF=\frac{10000}{\mbox{PlotSize }(m^2)}\,\]
For example, with a circular fixed area plot of 200 m² or 0.02 ha, the expansion factor is 50. The per-plot observations need to be expanded (multiplied) by \(EF=50\) to produce the per-hectare estimates. This expansion factor is the inverse of the inclusion probability resulting from a certain plot design.
The estimation procedure is illustrated with a simple example: assuming in a 5.0 ha forest stand, 5 plots with 500 m² each are randomly selected. The target variable is the number of stems and we are interested in the estimates per ha and in the estimated total, including the corresponding standard errors. After finishing the inventory, stems per plot observations are 20, 25, 30, 35 and 40 respectively for the 5 plots. It is important to note that each of the plots gives us exactly one independent estimation for the target variable.
The expansion factor is \(EF=20\). Therefore, the per-hectare values expanded from the per-plot values are then 400, 500, 600, 700 and 800, respectively. From these, mean number of stems per ha and its variance can be calculated.
Alternatively, and may be easier, we may calculate all estimations first on a per-plot basis and apply the expansion factor later. For this example, the results per plot are:
Mean number of stems per plot \(\bar{y}=30\,\) with variance per plot \(s^2=62.5\,\) and standard error \(s_y=\frac{sw}{\sqrt{n}}=\frac{7.91}{\sqrt{5}}=3.53\,\)
From the standard error, the confidence interval can be calculated where we use for convenience
\[t=2:\mbox{ }ts_y\approx2s_y=2*3.53=7.06\,\]
and therefore:
\[CI=\left[\left(\bar{y}-ts_{\bar{y}}\right)\le\mu\le\left(\bar{y}+ts_{\bar{y}}\right)\right]=\]
\[\left[\left(30-7.06\right)\le\mu\le\left(30+7.06\right)\right]=\left[22.94\le\mu\le37.06\right]\,\]
The results at per-hectare are simply derived by multiplying the per-plot results with the expansion factor, thus for example,
mean number of stems per hectare is \({\bar{y}}_{ha}=30*20=600\,\) and standard error is \(s_{\bar{y}ha}=3.53*20=70.6\mbox{ stems/ha}\,\).
Other estimations follow suit. However, when applying the expansion factor to the variance, it must be observed that the variance comes as squared figure so that the expansion needs to be done with \(EF^2\)! That is, in our example with an estimated per-plot variance of
\[s_{plot}^2=62.5\,\]
the estimated per-hectare variance is
\[s_{ha}^2=s_{plot}^2*EF^2=62.5*20^2=25000\,\]
Cluster plots
So far, we looked at fixed area plots as compact and coherent geometrical shapes like circle and rectangle. However, a sample plot can also come “in pieces”. The most typical examples are the so-called cluster plots (a more detailed description is in the article cluster sampling) which are usually employed in large area forest inventories. Each cluster plot consists of several subunits, called sub-plots, which are located at a certain defined distance apart from each other.
However, we wish to stress yet here that also for cluster plots it holds what was said about randomization and sample size: each randomization step yields one independently selected sample and each one of these such independently selected samples produces exactly one independent observation of the target variable. That means that the entire cluster plot produces one observation of, for example, basal area, and not each sub-plot! This is a frequently committed confusion in forest inventory sampling.
Nested sub-plots
Figure 3 shows a typical diameter distribution in a natural forest, where there is a very high number of small trees and fewer large trees; such a distribution is also called negatively J-shaped. If we lay out a single fixed area plot with a defined radius, our sample plot mirrors what this diameter distribution shows: we will include a high number of small trees and only very few larger trees. Usually, however, we are at least as much interested in the larger trees and do not like to have a very high number of small trees on the plot.
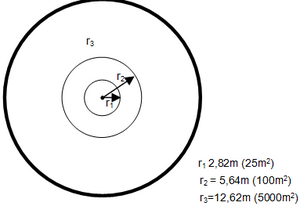
The solution to this is simple: we use nested sub-plots with different sizes as illustrated in Figure 4 for different size classes of trees each; usually, those size classes are diameter classes. Then we can define the plot size for different diameter classes such that in each class (nested sub-plot) there is more or less the target number of sample trees: plots with larger radii are used for larger sample trees and smaller plots for smaller trees.
Nested sub-plots segregate trees by diameter classes and the corresponding plot sizes are different; therefore, analysis must also be made separately for each plot size as there are different plot expansion factors depending on plot size.
The inclusion zone concept can immediately be applied also to nested circular sub-plots as illustrated in Figure 5. There (right hand side), the size of the inclusion zone depend on the diameter of the tree: smaller trees have a smaller inclusion zone and therefore also a smaller selection probability.
Nested sub-plots are not restricted to circular plots but can be applied to any plot shape. Figure 6 gives an illustration of various options. When strip plots are applied, the regeneration plot is frequently taken as a small circular plot of some few square meters. That means that also different plot shapes can be used for the differently sized plots.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.
- ↑ Prodan M., R. Peters, F. Cox and P. Real 1997. Mensura forestal. Serie investigación y educación en desarrollo sostenible. IICA/GTZ. 561p.