Importance sampling
Importance sampling is a sampling strategy that selects samples proportional to size – but not from a discrete population of single elements of which each has a selection probability. Importance sampling is applicable to continuous populations where the size attribute is a function from which a probability density function is derived.
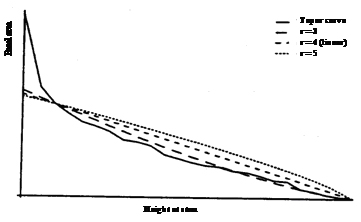
Typical application in forestry is estimating individual tree volume by sampling the taper curve: we imagine a taper curve is given, as for example, in Figure 2.
If A(h) is a function of basal area over height, the stem volume from the bottom to an upper height value \(H_u\) can be determined from
\[\int_{0}^{H_u} A(h) dh\]
This integral is now to be estimated by selecting some heights at which basal area measurements are taken. One could select simple uniformly distributed height values and thus assigning the same selection probabilities to low height values where there is a lot of wood volume and the upper height values where there is much less volume. It makes, obviously, sense to use unequal selection probabilities that are continuously decreasing from the bottom to the top of the stem.
To do that, we must develop a scheme how to define the selection probabilities. In list sampling for discrete elements, we could craft a list and assign selection probabilities proportional to an ancillary size variable. With a continuous population we must devise a continuous function from which to sample with unequal probabilities. It would be optimal to know the exact taper curve, because then, we would make a perfect estimate of the target variable volume or area below the curve (just as we would make a perfect estimate of the totals with the Hansen-Hurwitz estimator if the selection probabilities can be defined strictly proportional to the target variable). As we do not know the taper curve, we use a proxy. Figure 2 shows various options together with the true taper curve of a sample tree. To build the proxy probability density function one needs input information; what we usually have is dbh and height, so that the proxy taper function goes through these points, where the curve intersects with the abscissa at tree height (tree radius = 0).
A probability density function (pdf) must have various properties:
- it must have positive values on the interval ;
- it must be 0 outside that interval;
- and the integral on the range \([H_b , H_u]\) must be 1.
All these conditions, by the way, are also satisfied when simple random sampling is applied. If the range of possible values is from 1…R, then the probability density function is a parallel to the abscissa intersecting the ordinate at the value 1/R; by that, it is guaranteed that the total probability density under the curve is 1.0.
A linear pdf is possible (r=4 in Figure 2). If is stem length (or total height), then the linear pdf takes on the form
\[f(h) = \frac {2}{H_u} - \frac {2}{H_u^2} h \]
being defined on the range [0..\(H_u\)]
While the linear model works nicely in many cases, frequently a better approximation can be achieved by curves such as those of the form
\[ d(h) = D \left [ \frac {H-h}{H} \right ]^{\frac {2}{r}}\]
Three examples for different values of the coefficient r are depicted in Figure 2.
If we select n sample heights \(\theta_i\) according to the pdf \(f(\theta_i)\) and measure there basal area \(A(\theta_i)\), then the volume V of that particular tree is estimated by the Hansen-Hurwitz estimator
\[V = \frac {1}{n} \sum_{i=1}^n \frac {a(\theta_i}{f(\theta_i)}\]
We denote with \(V_p\) the volume that results from the proxy function \(A_p (h)\) on the interval from 0 to Hu. It is a biased volume as \(A_p (h)\) is but a proxy for the true function of basal area over height. The probability density function f(h) is then for
\[0 \le h \le H_u \, f(h) = \frac {A_p (h)}{V_p}\]
Then, the volume estimation from measurements at n Heights at the stem - selected according to the pdf f(h) - can be re-written as
\[\hat V = V_p \frac {1}{n}\sum_{i=1}^n \frac {A(\theta_i)}{A_p(\theta_i)}\]
where the expression to the right can be interpreted as a "calibration factor" which makes the estimation Vp unbiased.
The parametric error variance of volume estimation from a sample of size n is
\[var(\hat V) = \frac {1}{n} \int_{H_U}^{H_O} f(h) \left [ \frac {A(h)}{f(h)} - V \right ]^2 dh = \frac {1}{n} \int_{H_U}^{H_O} \frac {A^2(h)}{f(h)} dh - V\,\]
estimated from a sample of size n from
\[v\hat ar(\hat V) = \frac {1}{n(n-1)} \sum_{i=1}^n \left [ \frac {A(\theta_i)}{f(\theta_i)} - \hat V \right ]^2\].
For illustration: for a sampling study, the taper curve of various trees was accurately determined by many measurements. Then, it is possible to simulate different sampling approaches for the estimation of stem volume (Kleinn 1993 [1]). This was done for several hundred sample trees (spruce and Douglas fir). Then, the performance of different proxy functions (which define the unequal selection probabilities) was compared. The results are presented in Table 25. With simple random sampling the per-tree volume estimation with n = 1 has here a relative standard error of about 70% - which can, of course, only be determined by simulation, as a single sample of n = 1 does not allow estimating error variance. A linear probability density function (defined by tree height and the default measurement at breast height) yields a reduction of the relative standard error down to about 17%, which can still be improved by using a curvilinear probability density function (r=3 along the function given above; see also Table 2).
Table 2. Result from a simulation study on several hundred of trees (spruce and Douglas fir). Given is the mean relative error (cv%) of the volume estimate for importance sampling of individual trees with one measurement per tree (n=1) (from Kleinn 1993[1]). The estimations are given for different approaches to unequal probability sampling where the function \(d(h) = D \left [ \frac {H-h}{H} \right ]^{\frac {2}{r}}\) was used to define the shape of the proxy probability function. “Uniform” means simple random sampling from a uniform distribution of random numbers.
| ||||||||||||||||||||