Category talk:03 Electromagnetic radiation
| sorry: |
This section is still under construction! This article was last modified on 10/25/2013. If you have comments please use the Discussion page or contribute to the article! |
Contents |
Basic physical equations
Life on earth would be impossible without solar energy. The source of the sun's energy are nuclear fusion processes of hydrogen to helium. Electromagnetic radiation (EMR) is generated on the surface of the sun and carries solar energy through the space to the earth.
The phenomenon of EMR can be explained by two physical theories at the same time: the wave theory and the quantum theory.
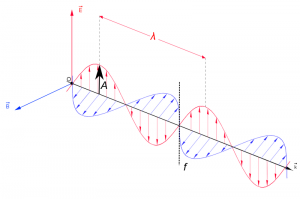
EMR can be seen as a wave with time-varying electric (E) and magnetic fields (B). These vector fields have a sine waveform, are oriented at right angles at each other and oscillate perpendicular to the direction of wave travel (Fig.).
where wavelength $\lambda$ = the distance between adjacent wave peaks measured in the unit lengths nanometer (1nm = 1x10-9m)or micrometer(1 mm=x 10-6m). Frequency f = number of peaks passing a fixed point in a given period of time measured in the unit Hertz (1 Hz = 1 cycle per second) Amplitude A = height of each peak and often measured as energy level (e.g. spectral irradiance [Watt per m2 per micrometer]) No medium is needed for the propagation of EMR waves. The speed of EMR in vacuum. \begin{equation} c=\lambda*f \end{equation} c is a universal constant (c $\approx$ 300 000 kilometer per second). Taking the mean distance between sun and earth ($\approx$ 150 000 000 km) it takes $\approx$ 8 minutes until solar EMR reaches the earth.
In the quantum theory EMR is composed of discrete packets of energy known as photons or quanta. They have no mass. Planck's formula allows to calculate the energy transported by a photon : \begin{equation} Q=h*f \end{equation} where Q=radiant energy of a photon measured in Joule [J] h = Planck‘s constant (6.626x10-34 Joule-Second J sec) f = frequency [h]
Combining eq(1) and eq(2) gives
\begin{equation}
Q=\frac{h*c}{\lambda}
\end{equation}
The longer the wavelength involved, the lower is the radiant energy of EMR. In remote sensing $ \lambda $ and f are used to divide the EMR spectrum in main divisions.
Cite error: Invalid <ref> tag;
refs with no content must have a name
The electromagnetic spectrum
Visible Optical
Sources of EMR
Interaction of EMR with the atmosphere
Why is the sky blue? Why is the sun red at sunset? When can we see a rainbow?
Interaction of EMR with the earth surface
Spectral reflectance patterns of the earth surface
Terms in radiation
Cite error:
<ref> tags exist, but no <references/> tag was found