The trigonometric principle

sorry:

This section is still under construction! This article was last modified on 11/4/2010. If you have comments please use the Discussion page or contribute to the article!

Basic principle

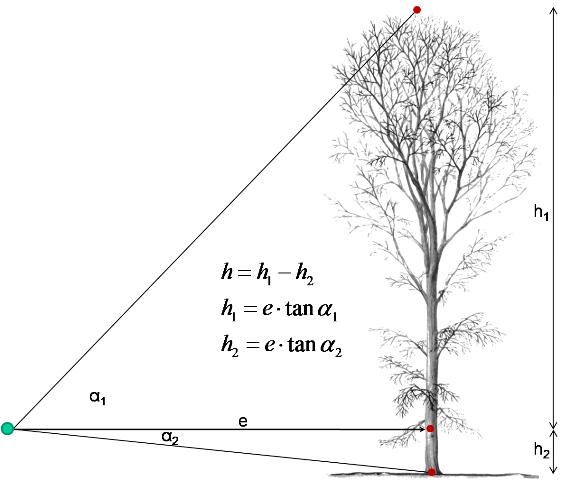
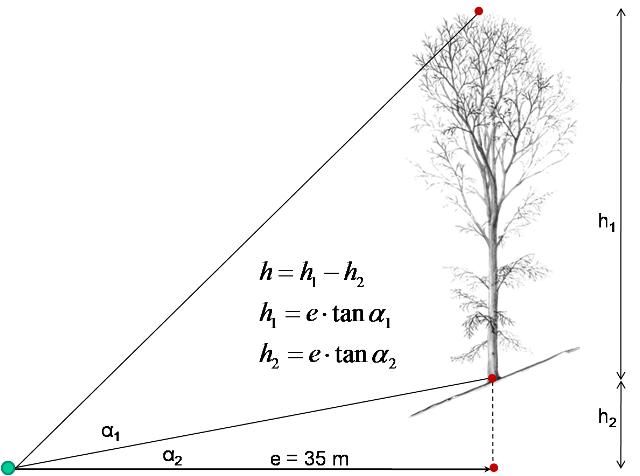
The so-called trigonometric principle of height measurement bases on the measurement of angles as illustrated in the following figure. Height values per inclination angle are then calculated by

\[h=e*\tan \alpha \,\],

if the inclination is measured in degrees or

\[h=e*\frac{p}{100} \,\],

if inclination is measured in percent; e is the horizontal distance. These basic formula allow calculating what is given as h1 and h2 in the figure.

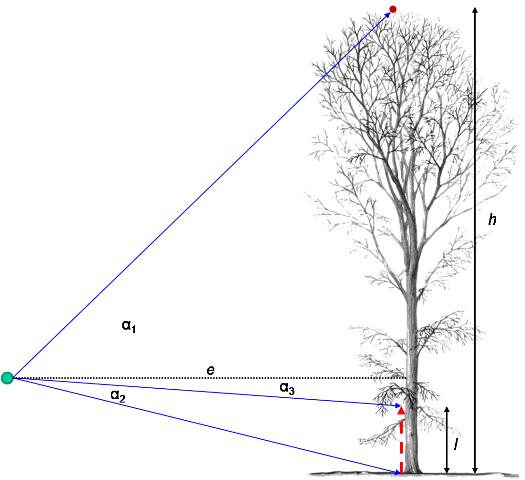
Measuring tree heights in sloped terrain

Note:

If one uses a measurement device which does not enable to directly measure horizontal distances (or e.g. rely on fixed distances to the tree determined by optical principles) the measured distance has to be corrected. To avoid corrections in sloped terrain a practical solution is to move parallel to the slope and to find a position from which one can directly measure the horizontal distance.

Measuring height without given distance