Estimation on changes
(→General observations) |
(→General observations) |
||
| Line 9: | Line 9: | ||
If repeated observations are made, estimation of change can be expressed as | If repeated observations are made, estimation of change can be expressed as | ||
| − | |||
:<math>change=c=\bar{y_2}-\bar{y_1},\,</math> | :<math>change=c=\bar{y_2}-\bar{y_1},\,</math> | ||
| − | |||
where <math>\bar{y_1}</math> is the estimated mean at point 2 in time and <math>\bar{y_1}</math> is the estimated mean at point 1 in time. The estimated change is a linear combination of two random variables, i.e. the two estimated means can be considered random variables and they are “linked” by the linear operator “minus”. Then, the expected value and the variance of this linear combination can be determined along the rules presented in the context of stratification (there, however, weighted estimated means were added, while here, estimated means are subtracted); in stratification, the random variables (the stratum estimated results) were independent random variables, while in change estimation we deal either with dependent or with independent random variables: | where <math>\bar{y_1}</math> is the estimated mean at point 2 in time and <math>\bar{y_1}</math> is the estimated mean at point 1 in time. The estimated change is a linear combination of two random variables, i.e. the two estimated means can be considered random variables and they are “linked” by the linear operator “minus”. Then, the expected value and the variance of this linear combination can be determined along the rules presented in the context of stratification (there, however, weighted estimated means were added, while here, estimated means are subtracted); in stratification, the random variables (the stratum estimated results) were independent random variables, while in change estimation we deal either with dependent or with independent random variables: | ||
*One may carry out an inventory in point 1 in time <math>t_1</math> and then another one independently of the first inventory in point 2 in time <math>t_2</math>. Independent means here that at the two points in time different randomizations were done, and, therefore, different sample plots selected. The change is estimated then along <math>c=\bar{y_2}-\bar{y_1}</math>, and the variance of the estimated change is the sum of the variances: | *One may carry out an inventory in point 1 in time <math>t_1</math> and then another one independently of the first inventory in point 2 in time <math>t_2</math>. Independent means here that at the two points in time different randomizations were done, and, therefore, different sample plots selected. The change is estimated then along <math>c=\bar{y_2}-\bar{y_1}</math>, and the variance of the estimated change is the sum of the variances: | ||
| − | |||
:<math>var(\bar{y_2}-\bar{y_1})=var\bar{y_1}+var{y_2}.\,</math> | :<math>var(\bar{y_2}-\bar{y_1})=var\bar{y_1}+var{y_2}.\,</math> | ||
| − | |||
*However, one may at point 2 in time revisit the same plots that were established in point 1 in time. These plots are called “permanent sample plots” and their position needs to be recorded and marked such that they can be found after a certain time period. In that case, the estimated means are not independent, because in point 2 in time there was not an independent sample selection, but the same plots were used as in point 1 in time. Or put in other words: for each observation in point 2 in time, we can exactly assign a corresponding observation from point 1 in time (that is: the observations from the same plot). In that case, change ''c'' is also estimated from <math>c=\bar{y_2}-\bar{y_1}</math>, but we need to take a covariance term in variance calculation into account: | *However, one may at point 2 in time revisit the same plots that were established in point 1 in time. These plots are called “permanent sample plots” and their position needs to be recorded and marked such that they can be found after a certain time period. In that case, the estimated means are not independent, because in point 2 in time there was not an independent sample selection, but the same plots were used as in point 1 in time. Or put in other words: for each observation in point 2 in time, we can exactly assign a corresponding observation from point 1 in time (that is: the observations from the same plot). In that case, change ''c'' is also estimated from <math>c=\bar{y_2}-\bar{y_1}</math>, but we need to take a covariance term in variance calculation into account: | ||
| − | |||
:<math>var(\bar{y_2}-\bar{y_1}=var\bar{y_2}+var\bar{y_1}-2cov(y_1y_2).\,</math> | :<math>var(\bar{y_2}-\bar{y_1}=var\bar{y_2}+var\bar{y_1}-2cov(y_1y_2).\,</math> | ||
| − | |||
As we are always interested in precise estimates, that is: low values for the variance, we may now wonder whether, given the same sample size in the two points in time, it is more recommendable to use dependent or independent inventories at the two points in time. The variances differ only in the covariance term. We may assume that the observations made on the same plot at different points in time are highly positively correlated (and have a high positive covariance). That means, in the case of dependent inventories (permanent plots) the covariance term is subtracted by the sum of the variances; leading to more precise estimates. This is actually conform with common sense considerations: in permanent inventories where the same plots are repeatedly observed, we can determine the differences (changes) for each plot – and not only for the entire population; we may, therefore, expect that this more detailed information leads also to more precise estimations of change. | As we are always interested in precise estimates, that is: low values for the variance, we may now wonder whether, given the same sample size in the two points in time, it is more recommendable to use dependent or independent inventories at the two points in time. The variances differ only in the covariance term. We may assume that the observations made on the same plot at different points in time are highly positively correlated (and have a high positive covariance). That means, in the case of dependent inventories (permanent plots) the covariance term is subtracted by the sum of the variances; leading to more precise estimates. This is actually conform with common sense considerations: in permanent inventories where the same plots are repeatedly observed, we can determine the differences (changes) for each plot – and not only for the entire population; we may, therefore, expect that this more detailed information leads also to more precise estimations of change. | ||
Revision as of 12:47, 11 March 2011
Contents |
General observations
In a “one-shot” forest inventory, the vast majority of measurements estimate the status quo for given attributes. However, estimation of changes is at least as important to evaluate the dynamics of the forest ecosystem and to monitor the silvicultural treatments and the performance of forest management.
There are only few change attributes that can be measured directly. Typical examples are increment borings, where the change (increment) of dbh over a certain period can directly be measured on a bore core and expanded to the entire cross section; and measurement of length of terminal shoots (or distances between whirls) for coniferous trees.
If repeated observations are made, estimation of change can be expressed as
\[change=c=\bar{y_2}-\bar{y_1},\,\]
where \(\bar{y_1}\) is the estimated mean at point 2 in time and \(\bar{y_1}\) is the estimated mean at point 1 in time. The estimated change is a linear combination of two random variables, i.e. the two estimated means can be considered random variables and they are “linked” by the linear operator “minus”. Then, the expected value and the variance of this linear combination can be determined along the rules presented in the context of stratification (there, however, weighted estimated means were added, while here, estimated means are subtracted); in stratification, the random variables (the stratum estimated results) were independent random variables, while in change estimation we deal either with dependent or with independent random variables:
- One may carry out an inventory in point 1 in time \(t_1\) and then another one independently of the first inventory in point 2 in time \(t_2\). Independent means here that at the two points in time different randomizations were done, and, therefore, different sample plots selected. The change is estimated then along \(c=\bar{y_2}-\bar{y_1}\), and the variance of the estimated change is the sum of the variances:
\[var(\bar{y_2}-\bar{y_1})=var\bar{y_1}+var{y_2}.\,\]
- However, one may at point 2 in time revisit the same plots that were established in point 1 in time. These plots are called “permanent sample plots” and their position needs to be recorded and marked such that they can be found after a certain time period. In that case, the estimated means are not independent, because in point 2 in time there was not an independent sample selection, but the same plots were used as in point 1 in time. Or put in other words: for each observation in point 2 in time, we can exactly assign a corresponding observation from point 1 in time (that is: the observations from the same plot). In that case, change c is also estimated from \(c=\bar{y_2}-\bar{y_1}\), but we need to take a covariance term in variance calculation into account:
\[var(\bar{y_2}-\bar{y_1}=var\bar{y_2}+var\bar{y_1}-2cov(y_1y_2).\,\]
As we are always interested in precise estimates, that is: low values for the variance, we may now wonder whether, given the same sample size in the two points in time, it is more recommendable to use dependent or independent inventories at the two points in time. The variances differ only in the covariance term. We may assume that the observations made on the same plot at different points in time are highly positively correlated (and have a high positive covariance). That means, in the case of dependent inventories (permanent plots) the covariance term is subtracted by the sum of the variances; leading to more precise estimates. This is actually conform with common sense considerations: in permanent inventories where the same plots are repeatedly observed, we can determine the differences (changes) for each plot – and not only for the entire population; we may, therefore, expect that this more detailed information leads also to more precise estimations of change.
Permanent plots
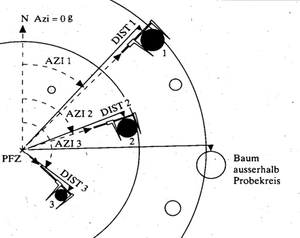
So-called permanent plots need to be installed when repeated observations of the same trees are to be made. While it is frequently said “we install permanent plots”, one will only see after the first re-measurement whether it is really permanent plots! It is more costly to install plots that are to be used as permanent plots because:
- The plot location needs to be marked and or recorded such that it can be found again after some time (usually several years. This is done by determining the GPS coordinates and by drawing a draft of the way to the plot.
- The trees need to be mapped on the plot so that changes per individual tree can be observed. On circular plots that is done by measuring azimuth and distance of the trees to the plot center. On strip plots, the position of each tree is determined by the length measurement on the central line of the strip and by measuring the distance from the center line; in that case: do not forget to also record whether the tree is on the right or left side of the center line … This tree map is also very helpful in finding the sample plot at the second point in time.
Figure 1 illustrates the position measurement of trees on a plot established as permanent plot. Here, dbh is measured with the caliper; in order to avoid that major discrepancies between the repeated measurements come from irregularities of the stem when different orientations of the caliper measurements at the two points in time were taken, in that inventory it was defined that all dbh measurements are to be taken such that the leg of the caliper points exactly to the plot center. Figure 2 illustrates a result plot map of re‑measured trees depicting the dbh of the trees and the change in dbh.
References
- ↑ Brändli U.B., A. Herold, H. Stierlin und J. Zinggeler 1994. Schweizerisches Landesforst-inventar. Anleitung für die Feldaufnahmen der Erhebung 1993-1995. Birmensdorf, Eidg. Forschungsanstalt für Wald, Schnee und Landschaft. 204 S.