Sampling intensity vs. sample size
(Created page with "{{Content Tree|HEADER=Forest Inventory lecturenotes|NAME=Forest Inventory lecturenotes}} ==General observations== [[File:3.7-fig44.png|right|thumb|300px|''...") |
|||
| Line 8: | Line 8: | ||
It happens sometimes that in prescriptions for [[Forest inventory|forest management inventories]] it is written that at least, say, 5% of the population needs to be sampled in order to achieve useful results. However, this rule is difficult, as 5% of the population may mean different sample sizes; and therefore, a clear conclusion about the standard error can hardly be drawn. It is better to talk about sample sizes and variances as these two factors are those which determine the standard error. | It happens sometimes that in prescriptions for [[Forest inventory|forest management inventories]] it is written that at least, say, 5% of the population needs to be sampled in order to achieve useful results. However, this rule is difficult, as 5% of the population may mean different sample sizes; and therefore, a clear conclusion about the standard error can hardly be drawn. It is better to talk about sample sizes and variances as these two factors are those which determine the standard error. | ||
| − | There is an interesting example in the scientific literature that illustrates this confusion of sample size and sampling intensity. According to Tucker and Townshend (2000), a satellite image based sample of 10% (as employed by FAO in the global forest assessment to estimate tropical deforestation; referring to the total number of Landsat scenes covering the tropical belt) is not sufficient. The authors proved by simulating deforestation estimations from a 10% sample using the example of Bolivia (where the entire country is covered by 41 Landsat scenes), that rather a full coverage would be required. | + | There is an interesting example in the scientific literature that illustrates this confusion of sample size and sampling intensity. According to Tucker and Townshend (2000<ref name="tucker_townshend2000>Tucker C.J. and J.R.G. Townshend 2000. Strategies for monitoring tropical deforestation using satellite data. International Journal of Remote Sensing 21:1461-1471.</ref>), a satellite image based sample of 10% (as employed by FAO in the global forest assessment to estimate tropical deforestation; referring to the total number of Landsat scenes covering the tropical belt) is not sufficient. The authors proved by simulating deforestation estimations from a 10% sample using the example of Bolivia (where the entire country is covered by 41 Landsat scenes), that rather a full coverage would be required. |
| − | + | ||
==Example== | ==Example== | ||
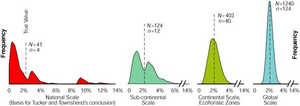
| − | In a response article, Czaplewski (2003) repeated and extended the experiment with the Bolivia data. The 10% sample, where 4 images were taken out of the 41 images covering Bolivia, was repeated many times. The resulting sample distribution for the national scale is given in Figure | + | In a response article, Czaplewski (2003<ref name="czaplewski2003">Czaplewski R. 2003. Can a sample of Landsat sensor scenes reliably estimate the global extent of tropical deforestation? International Journal of Remote Sensing 24(6):1409- 1412.</ref>) repeated and extended the experiment with the Bolivia data. The 10% sample, where 4 images were taken out of the 41 images covering Bolivia, was repeated many times. The resulting sample distribution for the national scale is given in Figure 1 on the left hand site. It is obvious that the precision is very poor as the resulting [[deforestation estimates]] show a high variation. As a consequence, the statements from Tucker and Townshend (2000<ref name="tucker_townshend2000>Tucker C.J. and J.R.G. Townshend 2000. Strategies for monitoring tropical deforestation using satellite data. International Journal of Remote Sensing 21:1461-1471.) are correct within the bounds of their experimental design (aerial extent of Bolivia!). |
| + | |||
| + | However, when investigating a larger scale like the sub-continental, the continental or the global one (like used by FAO) the given statements are not valid any longer. To proof this, Czaplewski (2003) created new data sets from the original 41 scenes by simply copying the 41 images several times, thus generating varying regional scales. From these new data sets again multiple 10% random samples were taken with the result that the sample distributions are getting narrower with increasing scale, which is of course a direct consequence of a higher absolute sample size (increasing form 4 to 124, see Figure 1) - while the sampling intensity keeps constant. The population characteristics (in terms of mean and variance) were exactly the same because all data sets were generated from the same images. Finally, for a population size of 1240 Landsat images, which approximately corresponds to the number of scenes that cover the tropical belt, the 10% sample corresponds to an absolute sample size of n=124; and in that case, the precision is very high. | ||
As a conclusion, one should avoid to state that a certain percentage of the population needs to be sampled to achieve valid results when not saying something about the population size or the minimum number of sample elements needed. Because the influence of sample intensity on the sample precision is an indirect one; which always interacts with the actual population size. | As a conclusion, one should avoid to state that a certain percentage of the population needs to be sampled to achieve valid results when not saying something about the population size or the minimum number of sample elements needed. Because the influence of sample intensity on the sample precision is an indirect one; which always interacts with the actual population size. | ||
| + | |||
==References== | ==References== | ||
<references/> | <references/> | ||
Revision as of 23:31, 9 March 2011
General observations
Sample size refers to the number n of sampling units that are selected from the population. Sampling intensity refers to the proportion of the population that is been sampled. It is important to realize that the standard error depends on sample size and not on sampling intensity. When sample size is large (although sampling intensity may be relatively small), one may expect precise results.
It happens sometimes that in prescriptions for forest management inventories it is written that at least, say, 5% of the population needs to be sampled in order to achieve useful results. However, this rule is difficult, as 5% of the population may mean different sample sizes; and therefore, a clear conclusion about the standard error can hardly be drawn. It is better to talk about sample sizes and variances as these two factors are those which determine the standard error.
There is an interesting example in the scientific literature that illustrates this confusion of sample size and sampling intensity. According to Tucker and Townshend (2000[2]), a satellite image based sample of 10% (as employed by FAO in the global forest assessment to estimate tropical deforestation; referring to the total number of Landsat scenes covering the tropical belt) is not sufficient. The authors proved by simulating deforestation estimations from a 10% sample using the example of Bolivia (where the entire country is covered by 41 Landsat scenes), that rather a full coverage would be required.
Example
In a response article, Czaplewski (2003[1]) repeated and extended the experiment with the Bolivia data. The 10% sample, where 4 images were taken out of the 41 images covering Bolivia, was repeated many times. The resulting sample distribution for the national scale is given in Figure 1 on the left hand site. It is obvious that the precision is very poor as the resulting deforestation estimates show a high variation. As a consequence, the statements from Tucker and Townshend (2000[3]
Cite error:
<ref> tags exist, but no <references/> tag was found