Stratified sampling examples
(→Example 1) |
(→Example 1) |
||
| Line 17: | Line 17: | ||
!''<math>\sigma_h^2\,</math>'' | !''<math>\sigma_h^2\,</math>'' | ||
|- | |- | ||
| − | |1 | + | |align="center"|'''1''' |
| − | |14 | + | |align="right"|14 |
| − | |4 | + | |align="right"|4 |
| − | |6.29 | + | |align="right"|6.29 |
| − | |3.49 | + | |align="right"|3.49 |
|- | |- | ||
| − | |2 | + | |align="center"|'''2''' |
| − | |8 | + | |align="right"|8 |
| − | |3 | + | |align="right"|3 |
| − | |10.13 | + | |align="right"|10.13 |
| − | |4.86 | + | |align="right"|4.86 |
|- | |- | ||
| − | |3 | + | |align="center"|'''3''' |
| − | |8 | + | |align="right"|8 |
| − | |3 | + | |align="right"|3 |
| − | |5.38 | + | |align="right"|5.38 |
| − | |2.48 | + | |align="right"|2.48 |
|} | |} | ||
| Line 49: | Line 49: | ||
!''mean*weight'' | !''mean*weight'' | ||
|- | |- | ||
| − | |1 | + | |align="center"|'''1''' |
| − | |6.29 | + | |align="right"|6.29 |
| − | |0.466667 | + | |align="right"|0.466667 |
| − | |2.9333 | + | |align="right"|2.9333 |
|- | |- | ||
| − | |2 | + | |align="center"|'''2''' |
| − | |10.13 | + | |align="right"|10.13 |
| − | |0.266667 | + | |align="right"|0.266667 |
| − | |2.7000 | + | |align="right"|2.7000 |
|- | |- | ||
| − | |3 | + | |align="center"|'''3''' |
| − | |5.38 | + | |align="right"|5.38 |
| − | |0.266667 | + | |align="right"|0.266667 |
| − | |1.4333 | + | |align="right"|1.4333 |
|- | |- | ||
| | | | ||
| Line 80: | Line 80: | ||
!''<math>var*W_h^2</math>'' | !''<math>var*W_h^2</math>'' | ||
|- | |- | ||
| − | |1 | + | |align="center"|'''1''' |
| − | |0.769230769 | + | |align="right"|0.769230769 |
| − | |0.87244898 | + | |align="right"|0.87244898 |
| − | |0.67111461 | + | |align="right"|0.67111461 |
| − | |0.146154 | + | |align="right"|0.146154 |
|- | |- | ||
| − | |2 | + | |align="center"|'''2''' |
| − | |0.714285714 | + | |align="right"|0.714285714 |
| − | |1.61979167 | + | |align="right"|1.61979167 |
| − | |1.15699405 | + | |align="right"|1.15699405 |
| − | |0.082275 | + | |align="right"|0.082275 |
|- | |- | ||
| − | |3 | + | |align="center"|'''3''' |
| − | |0.714285714 | + | |align="right"|0.714285714 |
| − | |0.82812500 | + | |align="right"|0.82812500 |
| − | |0.59151786 | + | |align="right"|0.59151786 |
| − | |0.042063 | + | |align="right"|0.042063 |
|- | |- | ||
| | | | ||
| Line 102: | Line 102: | ||
| | | | ||
|<math>var(\bar y)=</math> | |<math>var(\bar y)=</math> | ||
| − | |'''0.270492''' | + | |align="right"|'''0.270492''' |
|} | |} | ||
Revision as of 19:32, 16 December 2010
Example 1
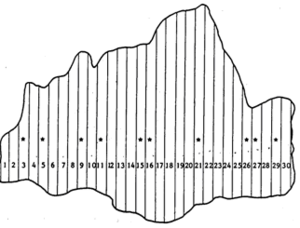
This example shows stratified sampling of the example population in figure 1.
Imagine the example population of \(N=30\) elements be subdivided into three strata as in figure 2. Here, stratification has been done arbitrarily into three strata of size 14, 8 and 8. From this stratified population, we wish to take a sample of \(n=10\), taking \(n_1=4\) from the first stratum and \(n_2=n_3=3\) from the other two strata. The stratum parametric means and variances are given in table 1.
Table 1 Stratum parameters for the stratified example population.
Stratum \(N_h\,\) \(n_h\,\) \(\mu_h\,\) \(\sigma_h^2\,\) 1 14 4 6.29 3.49 2 8 3 10.13 4.86 3 8 3 5.38 2.48
Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for \(n=10\) and the defined allocation of samples to the three strata.
Table 2 Calculation of parametric population mean from the parametric strata means.
Stratum Stratum mean Weight \((W_h)\) mean*weight 1 6.29 0.466667 2.9333 2 10.13 0.266667 2.7000 3 5.38 0.266667 1.4333 7.0667
Table 3 Calculation of parametric error variance of the estimated mean of the population for \(n=10\).
Stratum fpc \(\sigma_h^2/n\) var per stratum\(fpc*\sigma_h^2/n\) \(var*W_h^2\) 1 0.769230769 0.87244898 0.67111461 0.146154 2 0.714285714 1.61979167 1.15699405 0.082275 3 0.714285714 0.82812500 0.59151786 0.042063 \(var(\bar y)=\) 0.270492
The error variance of the estimated mean is
\(var(\bar y)=0.27049\)
which is considerably smaller than for simple random sampling with \(n=10\). That is: in this case, stratification makes sense and increases precision without increasing much the sampling effort. Stratification criteria must be known or decided on a priori.