Haralick Texture
From AWF-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
Image texture is a quantification of the spatial variation of grey tone values. Haralick | Image texture is a quantification of the spatial variation of grey tone values. Haralick | ||
| − | et al. (1973) | + | et al. (1973) suggested the use of gray level co-occurrence matrices (GLCM). This method is based on the joint probability distributions of pairs of pixels. GLCM show how often each gray level occurs at a pixel located at a fixed geometric position relative to each other pixel, as a function of the gray level (Srinivasan and Shobha 2008). An essential component is the definition of eight nearest-neighbor resolution cells (Fig.) that define different matrices for different angles (0°,45°,90°,135°) and distances between the horizontal neighboring pixels. uggested the use of gray level co-occurrence matrices(GLCM) |
| − | of the | + | |
| − | + | ||
| − | (Fig.) | + | |
| − | distances between the horizontal neighboring pixels. | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | of | + | |
| − | + | ||
| − | + | ||
[[File:Texture.png|center|500px|thumb|3x3 window definition and spatial relationship for calculating Haralick texture measures. Pixel 1 and 5 are 0° (horizontal) nearest neighbors to the center pixel * ; pixel 2 and 6 are 135° nearest neighbors; pixels 3 and 7 are 90° nearest neighbors, pixel 4 and 8 are 45° nearest neighbors to the center pixel * (Haralick et al. 1973)]] | [[File:Texture.png|center|500px|thumb|3x3 window definition and spatial relationship for calculating Haralick texture measures. Pixel 1 and 5 are 0° (horizontal) nearest neighbors to the center pixel * ; pixel 2 and 6 are 135° nearest neighbors; pixels 3 and 7 are 90° nearest neighbors, pixel 4 and 8 are 45° nearest neighbors to the center pixel * (Haralick et al. 1973)]] | ||
[[category:Spatial Filtering]] | [[category:Spatial Filtering]] | ||
Revision as of 21:16, 18 November 2017
Image texture is a quantification of the spatial variation of grey tone values. Haralick et al. (1973) suggested the use of gray level co-occurrence matrices (GLCM). This method is based on the joint probability distributions of pairs of pixels. GLCM show how often each gray level occurs at a pixel located at a fixed geometric position relative to each other pixel, as a function of the gray level (Srinivasan and Shobha 2008). An essential component is the definition of eight nearest-neighbor resolution cells (Fig.) that define different matrices for different angles (0°,45°,90°,135°) and distances between the horizontal neighboring pixels. uggested the use of gray level co-occurrence matrices(GLCM)
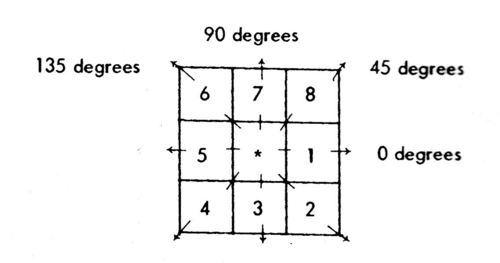
3x3 window definition and spatial relationship for calculating Haralick texture measures. Pixel 1 and 5 are 0° (horizontal) nearest neighbors to the center pixel * ; pixel 2 and 6 are 135° nearest neighbors; pixels 3 and 7 are 90° nearest neighbors, pixel 4 and 8 are 45° nearest neighbors to the center pixel * (Haralick et al. 1973)