Sampling intensity vs. sample size

Revision as of 23:31, 9 March 2011

General observations

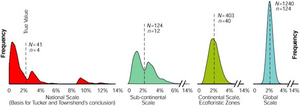
Figure 1 Distribution of sample based estimations of deforestation for Bolivia with 10% sampling intensity. Left: a wide range of estimated deforestation figures is produced when the original 41 Landsat scenes are taken as population. However, when these 41 images are simply 30 times copied (thus generating a much larger population but with exactly the same characteristics like mean and variance), then the 10% sample produces considerably much more precise results! (Czaplewski 2003^[1]).

Sample size refers to the number n of sampling units that are selected from the population. Sampling intensity refers to the proportion of the population that is been sampled. It is important to realize that the standard error depends on sample size and not on sampling intensity. When sample size is large (although sampling intensity may be relatively small), one may expect precise results.

It happens sometimes that in prescriptions for forest management inventories it is written that at least, say, 5% of the population needs to be sampled in order to achieve useful results. However, this rule is difficult, as 5% of the population may mean different sample sizes; and therefore, a clear conclusion about the standard error can hardly be drawn. It is better to talk about sample sizes and variances as these two factors are those which determine the standard error.

There is an interesting example in the scientific literature that illustrates this confusion of sample size and sampling intensity. According to Tucker and Townshend (2000^[2]), a satellite image based sample of 10% (as employed by FAO in the global forest assessment to estimate tropical deforestation; referring to the total number of Landsat scenes covering the tropical belt) is not sufficient. The authors proved by simulating deforestation estimations from a 10% sample using the example of Bolivia (where the entire country is covered by 41 Landsat scenes), that rather a full coverage would be required.

Example

In a response article, Czaplewski (2003^[1]) repeated and extended the experiment with the Bolivia data. The 10% sample, where 4 images were taken out of the 41 images covering Bolivia, was repeated many times. The resulting sample distribution for the national scale is given in Figure 1 on the left hand site. It is obvious that the precision is very poor as the resulting deforestation estimates show a high variation. As a consequence, the statements from Tucker and Townshend (2000^[3]