Stratified sampling examples
(→Example 1) |
|||
| Line 4: | Line 4: | ||
===Example 1=== | ===Example 1=== | ||
| − | This example shows stratified sampling of the example population in figure 1. | + | This example shows stratified sampling of the example [[population]] in figure 1. |
[[File:5.1.3-fig73.png|right|thumb|300px|'''Figure 1''' Example population (de Vries 1986<ref>de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. Springer. 399 p.</ref>)]] | [[File:5.1.3-fig73.png|right|thumb|300px|'''Figure 1''' Example population (de Vries 1986<ref>de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. Springer. 399 p.</ref>)]] | ||
| − | Imagine the example population of <math>N=30</math> elements be subdivided into three strata as in figure 2. Here, stratification has been done arbitrarily into three strata of size 14, 8 and 8. From this stratified population, we wish to take a sample of <math>n=10</math>, taking <math>n_1=4</math> from the first stratum and <math>n_2=n_3=3</math> from the other two strata. The stratum parametric means and variances are given in table 1. | + | Imagine the example population of <math>N=30</math> elements be subdivided into three [[strata]] as in figure 2. Here, stratification has been done arbitrarily into three strata of size 14, 8 and 8. From this stratified population, we wish to take a sample of <math>n=10</math>, taking <math>n_1=4</math> from the first stratum and <math>n_2=n_3=3</math> from the other two strata. The [[stratum parametric]] means and [[variance|variances]] are given in table 1. |
'''Table 1''' Stratum parameters for the stratified example population. | '''Table 1''' Stratum parameters for the stratified example population. | ||
| Line 41: | Line 41: | ||
[[File:5.2.6-fig75.png|right|thumb|300px|'''Figure 2''' Subdividing the example population (arbitrarily) in three strata, for illustration purposes]] | [[File:5.2.6-fig75.png|right|thumb|300px|'''Figure 2''' Subdividing the example population (arbitrarily) in three strata, for illustration purposes]] | ||
| − | Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for <math>n=10</math> and the defined allocation of samples to the three strata. | + | Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the [[mean]] is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric [[error variance]] for <math>n=10</math> and the defined allocation of samples to the three strata. |
'''Table 2''' Calculation of parametric population mean from the parametric strata means. | '''Table 2''' Calculation of parametric population mean from the parametric strata means. | ||
| Line 113: | Line 113: | ||
<math>var(\bar y)=0.27049</math> | <math>var(\bar y)=0.27049</math> | ||
| − | which is considerably smaller than for simple random sampling with <math>n=10</math>. That is: in this case, stratification makes sense and increases precision without increasing much the sampling effort. Stratification criteria must be known or decided on a priori. | + | which is considerably smaller than for [[simple random sampling]] with <math>n=10</math>. That is: in this case, stratification makes sense and increases [[precision]] without increasing much the [[Category:Sampling techniques|sampling]] effort. Stratification criteria must be known or decided on a priori. |
==References== | ==References== | ||
Revision as of 17:08, 17 December 2010
| Languages: |
English |
Example 1
This example shows stratified sampling of the example population in figure 1.
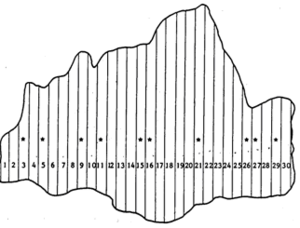
Imagine the example population of \(N=30\) elements be subdivided into three strata as in figure 2. Here, stratification has been done arbitrarily into three strata of size 14, 8 and 8. From this stratified population, we wish to take a sample of \(n=10\), taking \(n_1=4\) from the first stratum and \(n_2=n_3=3\) from the other two strata. The stratum parametric means and variances are given in table 1.
Table 1 Stratum parameters for the stratified example population.
Stratum \(N_h\,\) \(n_h\,\) \(\mu_h\,\) \(\sigma_h^2\,\) 1 14 4 6.29 3.49 2 8 3 10.13 4.86 3 8 3 5.38 2.48
Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for \(n=10\) and the defined allocation of samples to the three strata.
Table 2 Calculation of parametric population mean from the parametric strata means.
Stratum Stratum mean Weight \((W_h)\) mean*weight 1 6.29 0.466667 2.9333 2 10.13 0.266667 2.7000 3 5.38 0.266667 1.4333 7.0667
Table 3 Calculation of parametric error variance of the estimated mean of the population for \(n=10\).
Stratum fpc \(\sigma_h^2/n\) var per stratum\(fpc*\sigma_h^2/n\) \(var*W_h^2\) 1 0.769230769 0.87244898 0.67111461 0.146154 2 0.714285714 1.61979167 1.15699405 0.082275 3 0.714285714 0.82812500 0.59151786 0.042063 \(var(\bar y)=\) 0.270492
The error variance of the estimated mean is
\(var(\bar y)=0.27049\)
which is considerably smaller than for simple random sampling with \(n=10\). That is: in this case, stratification makes sense and increases precision without increasing much the effort. Stratification criteria must be known or decided on a priori.
References
- ↑ de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. Springer. 399 p.
- 2. Kleinn, C. 2007. Lecture Notes for the Teaching Module Forest Inventory. Department of Forest Inventory and Remote Sensing. Faculty of Forest Science and Forest Ecology, Georg-August-Universität Göttingen. 164 S.
