Electromagnetic radiation
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{construction}}{{Rscontent}} | + | {{construction}}{{Rscontent}}{{author|name=[[User:Hfuchs|Dr. Hans Fuchs]]}} |
==Basic physical equations== | ==Basic physical equations== | ||
| Line 5: | Line 5: | ||
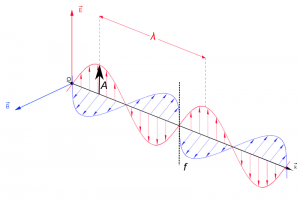
[[File:Onde_EMR.png|right|thumb|300px|'''Figure 1''' Snapshot of EMR wave model where | [[File:Onde_EMR.png|right|thumb|300px|'''Figure 1''' Snapshot of EMR wave model where | ||
$\lambda$ = wavelength, ''f'' = frequency and ''A'' = amplitude.]] | $\lambda$ = wavelength, ''f'' = frequency and ''A'' = amplitude.]] | ||
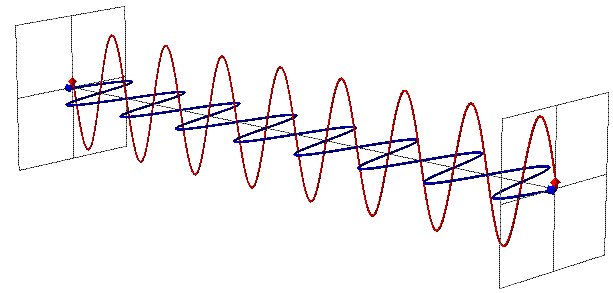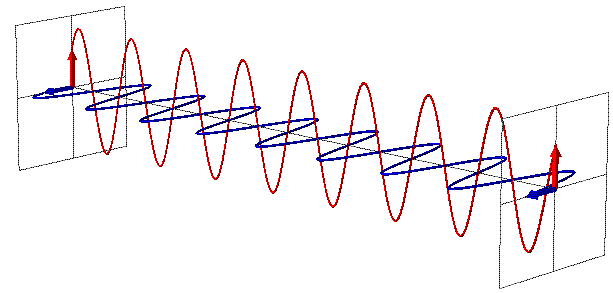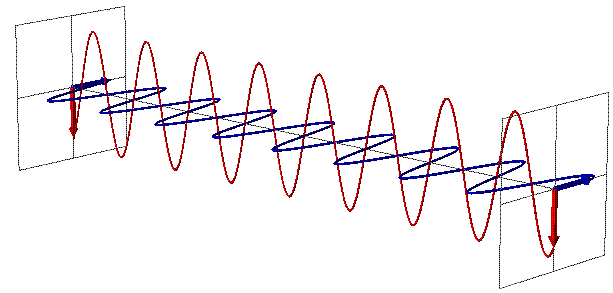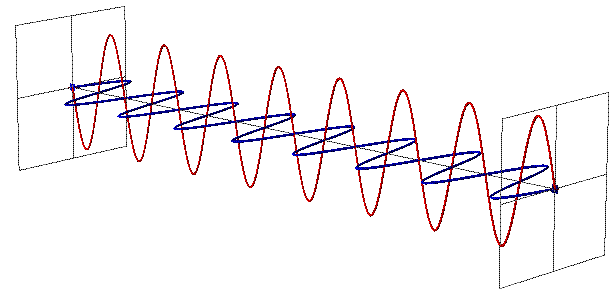
| − | [[File: | + | [[File:radiation2.gif|right|['''Figure 2''' 3D animation of EMR wave propagation.[http://www.mpoweruk.com/radio.htm Electropaedia]]] |
Life on earth would be impossible without solar energy. The source of the sun's energy are nuclear fusion processes of hydrogen to helium. Electromagnetic radiation (EMR) is generated on the hot surface of the sun and carries solar energy through the space to the earth. | Life on earth would be impossible without solar energy. The source of the sun's energy are nuclear fusion processes of hydrogen to helium. Electromagnetic radiation (EMR) is generated on the hot surface of the sun and carries solar energy through the space to the earth. | ||
The phenomenon of EMR can be explained by two physical theories at the same time: the wave theory and the quantum theory. | The phenomenon of EMR can be explained by two physical theories at the same time: the wave theory and the quantum theory. | ||
| − | EMR can be seen as a wave with time-varying electric (E) and magnetic fields (B). These vector fields have a sine waveform, are oriented at right angles at each other and oscillate perpendicular to the direction of wave travel (Fig. 1). Waves are characterized by | + | EMR can be seen as a wave with time-varying electric (E) and magnetic fields (B). These vector fields have a sine waveform, are oriented at right angles at each other and oscillate perpendicular to the direction of wave travel (Fig. 1 and Fig. 2). Waves are characterized by: |
| − | *wavelength $\lambda$ = the distance between adjacent wave peaks measured in the unit lengths nanometer (1nm = | + | *wavelength $\lambda$ = the distance between adjacent wave peaks measured in the unit lengths nanometer ($1nm = 1*10^{-9}m$) or micrometer ($1 micron = 1 \mu m = 1*10^{-6}m$) |
*frequency ''f'' = number of peaks passing a fixed point in a given period of time measured in the unit Hertz (1 Hz = 1 cycle per second) | *frequency ''f'' = number of peaks passing a fixed point in a given period of time measured in the unit Hertz (1 Hz = 1 cycle per second) | ||
| − | *amplitude ''A'' = height of each peak and often measured as energy level (e.g. spectral irradiance (Watt per | + | *amplitude ''A'' = height of each peak and often measured as energy level (e.g. spectral irradiance (Watt per $m^2$ per micrometer)). |
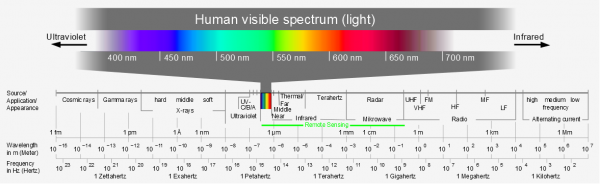
$ \lambda $ and ''f'' are used to divide the [[The electromagnetic spectrum|electromagnetic spectrum]] in main divisions. | $ \lambda $ and ''f'' are used to divide the [[The electromagnetic spectrum|electromagnetic spectrum]] in main divisions. | ||
No medium is needed for the propagation of EMR waves. The [[wikipedia:speed of light|speed of light]] ''c'' in vacuum | No medium is needed for the propagation of EMR waves. The [[wikipedia:speed of light|speed of light]] ''c'' in vacuum | ||
| − | + | <math> | |
c=\lambda*f | c=\lambda*f | ||
| − | + | </math> | |
is a universal constant (c $\approx$ 300 000 kilometer per second). Taking the mean distance between sun and earth ($\approx$ 150 000 000 km) it takes $\approx$ 8 minutes until solar EMR reaches the earth. | is a universal constant (c $\approx$ 300 000 kilometer per second). Taking the mean distance between sun and earth ($\approx$ 150 000 000 km) it takes $\approx$ 8 minutes until solar EMR reaches the earth. | ||
| − | In the quantum theory EMR is composed of discrete packets of energy known as photons or quanta. They have no mass. Planck's formula allows to calculate the energy transported by a single photon : | + | In the quantum theory EMR is composed of discrete packets of energy known as photons or quanta. They have no mass. Planck's formula allows to calculate the energy transported by a single photon: |
\begin{equation} | \begin{equation} | ||
Q=h*f | Q=h*f | ||
| Line 28: | Line 28: | ||
where | where | ||
*''Q''=radiant energy of a photon measured in Joule (J) | *''Q''=radiant energy of a photon measured in Joule (J) | ||
| − | *''h'' = Planck‘s constant (6. | + | *''h'' = Planck‘s constant ($6.626*10^{-34}$ Joule-Second (J sec) |
*''f'' = frequency (hz) | *''f'' = frequency (hz) | ||
| Line 37: | Line 37: | ||
The longer the wavelength involved, the lower is the radiant energy of EMR and the lower is the frequency. | The longer the wavelength involved, the lower is the radiant energy of EMR and the lower is the frequency. | ||
| − | Electromagnetic energy is produced whenever a charged particle such as an electron or a nucleus of an atom changes its velocity and internal energy status. Every substance with a temperature above the absolute zero (0 K or -273.16°C) produces radiant energy and emits EMR in a | + | Electromagnetic energy is produced whenever a charged particle such as an electron or a nucleus of an atom changes its velocity and internal energy status. Every substance with a temperature above the absolute zero (0 K or -273.16°C) produces radiant energy and emits EMR in a continuous spectrum of wavelengths. The higher the temperature the higher is the motion of electrons, molecules and atoms. Not all materials heated to the same temperature emit the same amount and spectral composition of EMR. This is not the case for an hypothetical perfect absorber and re-emitter of energy. Such an object is called blackbody which absorbs and emits all radiation of wavelengths. Plank's radiation equation describes the radiant spectral exitance per unit wavelength $M_{\lambda}$ of a blackbody as: |
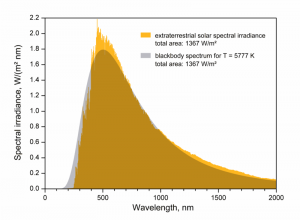
[[File:EffectiveTemperature_300dpi_e.png|right|thumb|300px|'''Figure 3''' Extraterrestrial solar irradiance at the top of atmosphere and spectral exitance curve of a blackbody at the temperature 5777K.]] | [[File:EffectiveTemperature_300dpi_e.png|right|thumb|300px|'''Figure 3''' Extraterrestrial solar irradiance at the top of atmosphere and spectral exitance curve of a blackbody at the temperature 5777K.]] | ||
| Line 44: | Line 44: | ||
\end{equation} | \end{equation} | ||
where | where | ||
| − | *$c_{1} | + | *$c_{1}=3.742*10^{-16} Wm^{-2}$ |
| − | *$c_{2} | + | *$c_{2}=1.4388*10^{-2} mK$ |
*$\lambda$=wavelength ($\mu$m) | *$\lambda$=wavelength ($\mu$m) | ||
*$T$=temperature (K) | *$T$=temperature (K) | ||
| Line 52: | Line 52: | ||
Fig. 3 shows that the sun can be approximated by a blackbody. | Fig. 3 shows that the sun can be approximated by a blackbody. | ||
| − | The first derivative of Planck's blackbody radiation equation determines the single maximum of the curve or the | + | The first derivative of Planck's blackbody radiation equation determines the single maximum of the curve or the wavelength of peak radiant exitance of a blackbody which is known as Wien's displacement equation: |
\begin{equation} | \begin{equation} | ||
\lambda_{max}=\frac{c_{3}}{T} | \lambda_{max}=\frac{c_{3}}{T} | ||
\end{equation} | \end{equation} | ||
where | where | ||
| − | *$c_{2} | + | *$c_{2}=2.89*10^{-3} mK$ |
| − | It shows that the | + | It shows that the wavelength of peak radiant exitance moves to shorter wavelengths with increasing temperature. The solar maximum irradiance occurs in the visible spectrum at 0.47$\mu$m. |
If we integrate the spectral radiant exitance curve of a blackbody over all wavelengths we obtain the total radiant energy exitance per unit surface area of the Stefan-Boltz-Mann equation: | If we integrate the spectral radiant exitance curve of a blackbody over all wavelengths we obtain the total radiant energy exitance per unit surface area of the Stefan-Boltz-Mann equation: | ||
| Line 65: | Line 65: | ||
\end{equation} | \end{equation} | ||
where | where | ||
| − | *$\alpha | + | *$\alpha=5.46697*10^-8 Wm^-2K^-4$ |
We assume a measured solar total radiant energy exitance per unit surface area on earth of about 1367 W/m2. This value is known as the solar constant also it varies throughout the year by about 3.5%. According to eq. 4 the total radiant exitance of an object depends only on the temperature and therefore the sun's temperature is estimated to 5777K. | We assume a measured solar total radiant energy exitance per unit surface area on earth of about 1367 W/m2. This value is known as the solar constant also it varies throughout the year by about 3.5%. According to eq. 4 the total radiant exitance of an object depends only on the temperature and therefore the sun's temperature is estimated to 5777K. | ||
| Line 73: | Line 73: | ||
Visible | Visible | ||
Optical | Optical | ||
| − | + | [[File:Electromagnetic_spectrum_modified.png|right|thumb|600px|'''Figure 3''' Main divisions of the electromagnetic spectrum]] | |
==Sources of EMR== | ==Sources of EMR== | ||
| Line 84: | Line 84: | ||
==Spectral reflectance patterns of the earth surface== | ==Spectral reflectance patterns of the earth surface== | ||
==Terms in radiation== | ==Terms in radiation== | ||
| − | [[category:Electromagnetic radiation]] | + | [[category:03 Electromagnetic radiation]] |
Latest revision as of 13:42, 2 November 2014
| sorry: |
This section is still under construction! This article was last modified on 11/2/2014. If you have comments please use the Discussion page or contribute to the article! |
Author of this article: Dr. Hans Fuchs
Contents |
[edit] Basic physical equations
Life on earth would be impossible without solar energy. The source of the sun's energy are nuclear fusion processes of hydrogen to helium. Electromagnetic radiation (EMR) is generated on the hot surface of the sun and carries solar energy through the space to the earth.
The phenomenon of EMR can be explained by two physical theories at the same time: the wave theory and the quantum theory.
EMR can be seen as a wave with time-varying electric (E) and magnetic fields (B). These vector fields have a sine waveform, are oriented at right angles at each other and oscillate perpendicular to the direction of wave travel (Fig. 1 and Fig. 2). Waves are characterized by:
- wavelength $\lambda$ = the distance between adjacent wave peaks measured in the unit lengths nanometer ($1nm = 1*10^{-9}m$) or micrometer ($1 micron = 1 \mu m = 1*10^{-6}m$)
- frequency f = number of peaks passing a fixed point in a given period of time measured in the unit Hertz (1 Hz = 1 cycle per second)
- amplitude A = height of each peak and often measured as energy level (e.g. spectral irradiance (Watt per $m^2$ per micrometer)).
$ \lambda $ and f are used to divide the electromagnetic spectrum in main divisions.
No medium is needed for the propagation of EMR waves. The speed of light c in vacuum \( c=\lambda*f \) is a universal constant (c $\approx$ 300 000 kilometer per second). Taking the mean distance between sun and earth ($\approx$ 150 000 000 km) it takes $\approx$ 8 minutes until solar EMR reaches the earth.
In the quantum theory EMR is composed of discrete packets of energy known as photons or quanta. They have no mass. Planck's formula allows to calculate the energy transported by a single photon: \begin{equation} Q=h*f \end{equation} where
- Q=radiant energy of a photon measured in Joule (J)
- h = Planck‘s constant ($6.626*10^{-34}$ Joule-Second (J sec)
- f = frequency (hz)
Combining eq(1) and eq(2) gives \begin{equation} Q=\frac{h*c}{\lambda} \end{equation} The longer the wavelength involved, the lower is the radiant energy of EMR and the lower is the frequency.
Electromagnetic energy is produced whenever a charged particle such as an electron or a nucleus of an atom changes its velocity and internal energy status. Every substance with a temperature above the absolute zero (0 K or -273.16°C) produces radiant energy and emits EMR in a continuous spectrum of wavelengths. The higher the temperature the higher is the motion of electrons, molecules and atoms. Not all materials heated to the same temperature emit the same amount and spectral composition of EMR. This is not the case for an hypothetical perfect absorber and re-emitter of energy. Such an object is called blackbody which absorbs and emits all radiation of wavelengths. Plank's radiation equation describes the radiant spectral exitance per unit wavelength $M_{\lambda}$ of a blackbody as:
\begin{equation} M_{\lambda}=\frac{c_{1}}{\lambda^{5}(exp(c_{2}/\lambda \ast T)-1)} \end{equation} where
- $c_{1}=3.742*10^{-16} Wm^{-2}$
- $c_{2}=1.4388*10^{-2} mK$
- $\lambda$=wavelength ($\mu$m)
- $T$=temperature (K)
. Fig. 3 shows that the sun can be approximated by a blackbody.
The first derivative of Planck's blackbody radiation equation determines the single maximum of the curve or the wavelength of peak radiant exitance of a blackbody which is known as Wien's displacement equation: \begin{equation} \lambda_{max}=\frac{c_{3}}{T} \end{equation} where
- $c_{2}=2.89*10^{-3} mK$
It shows that the wavelength of peak radiant exitance moves to shorter wavelengths with increasing temperature. The solar maximum irradiance occurs in the visible spectrum at 0.47$\mu$m.
If we integrate the spectral radiant exitance curve of a blackbody over all wavelengths we obtain the total radiant energy exitance per unit surface area of the Stefan-Boltz-Mann equation: \begin{equation} M=\alpha\ast T^{4} \end{equation} where
- $\alpha=5.46697*10^-8 Wm^-2K^-4$
We assume a measured solar total radiant energy exitance per unit surface area on earth of about 1367 W/m2. This value is known as the solar constant also it varies throughout the year by about 3.5%. According to eq. 4 the total radiant exitance of an object depends only on the temperature and therefore the sun's temperature is estimated to 5777K.
Kirchhoff's equation, emissivity, white body, gray body
[edit] The electromagnetic spectrum
Visible Optical
[edit] Sources of EMR
[edit] Interaction of EMR with the atmosphere
Why is the sky blue? Why is the sun red at sunset? When can we see a rainbow?