Stratified sampling examples
(→Example 1) |
(→Example 1) |
||
| Line 1: | Line 1: | ||
===Example 1=== | ===Example 1=== | ||
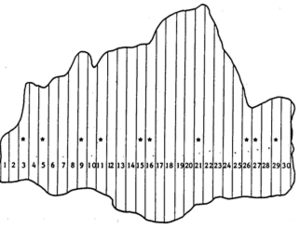
| − | This example shows stratified sampling | + | This example shows stratified sampling of the example population in figure 1. |
[[File:5.1.3-fig73.png|right|thumb|300px|'''Figure 1''' Example population (deVries 1986)]] | [[File:5.1.3-fig73.png|right|thumb|300px|'''Figure 1''' Example population (deVries 1986)]] | ||
| Line 36: | Line 36: | ||
|} | |} | ||
| − | [[File:5.2.6-fig75.png|right|thumb|300px|'''Figure 2''' Subdividing | + | [[File:5.2.6-fig75.png|right|thumb|300px|'''Figure 2''' Subdividing the example population (arbitrarily) in three strata, for illustration purposes]] |
Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for <math>n=10</math> and the defined allocation of samples to the three strata. | Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for <math>n=10</math> and the defined allocation of samples to the three strata. | ||
Revision as of 19:25, 16 December 2010
Example 1
This example shows stratified sampling of the example population in figure 1.
Imagine the example population of \(N=30\) elements be subdivided into three strata as in figure 2. Here, stratification has been done arbitrarily into three strata of size 14, 8 and 8. From this stratified population, we wish to take a sample of \(n=10\), taking \(n_1=4\) from the first stratum and \(n_2=n_3=3\) from the other two strata. The stratum parametric means and variances are given in table 1.
Table 1 Stratum parameters for the stratified example population.
| Stratum | \(N_h\,\) | \(n_h\,\) | \(\mu_h\,\) | \(\sigma_h^2\,\) |
|---|---|---|---|---|
| 1 | 14 | 4 | 6.29 | 3.49 |
| 2 | 8 | 3 | 10.13 | 4.86 |
| 3 | 8 | 3 | 5.38 | 2.48 |
Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for \(n=10\) and the defined allocation of samples to the three strata.
Table 2 Calculation of parametric population mean from the parametric strata means.
| Stratum | Stratum mean | Weight \((W_h)\) | mean*weight |
|---|---|---|---|
| 1 | 6.29 | 0.466667 | 2.9333 |
| 2 | 10.13 | 0.266667 | 2.7000 |
| 3 | 5.38 | 0.266667 | 1.4333 |
| 7.0667 |
Table 3 Calculation of parametric error variance of the estimated mean of the population for \(n=10\).
| Stratum | fpc | \(\sigma_h^2/n\) | var per stratum\(fpc*\sigma_h^2/n\) | \(var*W_h^2\) |
|---|---|---|---|---|
| 1 | 0.769230769 | 0.87244898 | 0.67111461 | 0.146154 |
| 2 | 0.714285714 | 1.61979167 | 1.15699405 | 0.082275 |
| 3 | 0.714285714 | 0.82812500 | 0.59151786 | 0.042063 |
| \(var(\bar y)=\) | 0.270492 |
The error variance of the estimated mean is \(var(\bar y)=0.27049\) which is considerably smaller than for simple random sampling with \(n=10\). That is: in this case, stratification makes sense and increases precision without increasing much the sampling effort. Stratification criteria must be known or decided on a priori.