Stratified sampling examples
(→Example 1) |
(→Example 1) |
||
| Line 48: | Line 48: | ||
Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for <math>n=10</math> and the defined allocation of samples to the three strata. | Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for <math>n=10</math> and the defined allocation of samples to the three strata. | ||
| + | |||
| + | '''Table 2:''' Calculation of parametric population mean from the parametric strata means. | ||
| + | |||
| + | <blockquote> | ||
| + | <div style="float:left; margin-right:2em"> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !''Stratum'' | ||
| + | !''Stratum mean'' | ||
| + | !''Weight <math>W_h\,</math>'' | ||
| + | !''mean<math>\by\,</math>weight'' | ||
| + | |- | ||
| + | |1 | ||
| + | |6.29 | ||
| + | |0.466667 | ||
| + | |2.9333 | ||
| + | |- | ||
| + | |2 | ||
| + | |10.13 | ||
| + | |0.266667 | ||
| + | |2.7000 | ||
| + | |- | ||
| + | |3 | ||
| + | |5.38 | ||
| + | |0.266667 | ||
| + | |1.4333 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |'''7.0667''' | ||
| + | |} | ||
| + | </div> | ||
Revision as of 18:47, 16 December 2010
Example 1
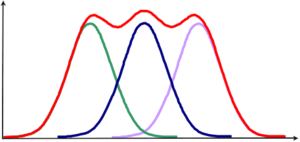
Imagine the example population of \(N=30\) elements be subdivided into three strata as in figure 1. Here, stratification has been done arbitrarily into three strata of size 14, 8 and 8. From this stratified population, we wish to take a sample of \(n=10\), taking \(n_1=4\) from the first stratum and \(n_2=n_3=3\) from the other two strata. The stratum parametric means and variances are given in Table 1.
Table 1: Stratum parameters for the stratified example population.
Stratum \(N_h\,\) \(n_h\,\) \(\mu_h\,\) \(\sigma_h^2\,\) 1 14 4 6.29 3.49 2 8 3 10.13 4.86 3 8 3 5.38 2.48
Calculation in stratified sampling is best done in tabular format, first per stratum and then combining the per-stratum results to the values / estimations for the entire population. The estimation of the mean is illustrated in Table 2 and results – as expected – in the parametric mean without stratification. Table 3 presents the calculation of the parametric error variance for \(n=10\) and the defined allocation of samples to the three strata.
Table 2: Calculation of parametric population mean from the parametric strata means.
Stratum Stratum mean Weight \(W_h\,\) mean\(\by\,\)weight 1 6.29 0.466667 2.9333 2 10.13 0.266667 2.7000 3 5.38 0.266667 1.4333 7.0667
sorry: This section is still under construction! This article was last modified on 12/16/2010. If you have comments please use the Discussion page or contribute to the article!