Accuracy and precision

Revision as of 11:08, 4 November 2013

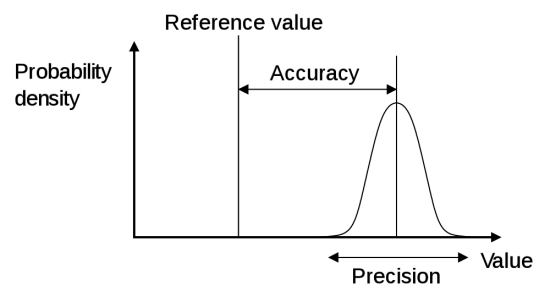
Accuracy and precision are two terms that are often equivalently used, even though they do not have the same meaning and should be used accordingly. The accuracy of estimates is the degree of "closeness" to the actual (true) value, while the precision of estimates is the degree to which repeated estimates under unchanged conditions show the same results. A simple definition of “accuracy” is therefore the freedom from mistake or error: correctness. While “precision” is defined as the quality or state of being precise: exactness.

Example:

Accuracy: Imagine you have the task to assess the mean height of students in a class. Unfortunately all you have for measuring the height is an old ruler, that has gotten a little longer with time. Thus, a bias is introduced by systematically underestimating the real height of each student. As a result the mean height estimated for the whole class will also be too low. Here we say: the accuracy of the height estimate is is low (even if the precision of estimates can be high). Precision: Using a ruler (which varies its length due to bad manufacturing), you want to measure your own height. While measuring your height several times in a row, you recognize that you measure a different height with every measurement. The variation of each measurement around the mean height (your real height) gives you an idea about the precision of the measurement.

Expressed in a more statistical formulation, we can say that precision is a qualitative measure of variability (or the sample distribution) of estimates around a mean, while accuracy can be described as deviation between the mean of estimates and the true target parameter. A measure of precision is the standard error of estimates.

• 

  High accuracy, low precision

• 

  Low accuracy, high precision

Related articles

• Random sampling example in the QGIS tutorial.