Ratio estimator
(Created page with "{{Languages}} {{Content Tree|HEADER=Forest Inventory lecturenotes|NAME=Forest Inventory lecturenotes}} __TOC__ ==Introduction== [[File:5.6.1-fig93.png|right|thumb|300px|'''Figu...") |
(→Introduction) |
||
| Line 7: | Line 7: | ||
[[File:5.6.1-fig93.png|right|thumb|300px|'''Figure 1''' Example of a population of 30 unequally sized strip plots; here, the ratio estimator may be applied for estimation using plot size as co-variable (DeVries 1986<ref>de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. Springer. 399 p.</ref>).]] | [[File:5.6.1-fig93.png|right|thumb|300px|'''Figure 1''' Example of a population of 30 unequally sized strip plots; here, the ratio estimator may be applied for estimation using plot size as co-variable (DeVries 1986<ref>de Vries, P.G., 1986. Sampling Theory for Forest Inventory. A Teach-Yourself Course. Springer. 399 p.</ref>).]] | ||
| − | There are situations in forest inventory sampling in which the value of the target variable is known (or suspected) to be highly correlated to an other variable (called co-variable or ancillary variable). We know from the discussion on spatial autocorrelation | + | There are situations in forest inventory sampling in which the value of the target variable is known (or suspected) to be highly correlated to an other variable (called co-variable or ancillary variable). We know from the discussion on [[spatial autocorrelation]] and the optimization of [[Cluster sampling|cluster plot design]] that correlation between two variables means essentially that the one variable does yet contain a certain amount of information about the other variable. The higher the correlation the better can the value of the second variable be predicted when the value of the first is known (and vice versa). Therefore, if such a co-variable is there on the plot, it would make sense to also observe it and utilize the correlation to the target variable to eventually improve the precision of estimating the target variable. This is exactly the situation where the ratio estimator is applied. |
| − | + | ||
| + | A typical and basic example is that of sample plots of unequal size, as depicted, for example in Figure 1 where strips of different length constitute the population of samples. Another example would be clusters of unequal size: while [[cluster sampling]] only deals with the case of clusters of equal size, the ratio estimator allows to take into account the differently sized sample plots. Here, obviously, the size of the sample plots is the co-variable that needs to be determined for each sample plot. That a high positive correlation is to be expected between most forestry-relevant attributes and plot size should be obvious: the larger the plot the more basal area, number of stems, volume etc. is expected to be present. | ||
==References== | ==References== | ||
{{Construction}} | {{Construction}} | ||
Revision as of 19:39, 29 December 2010
| Languages: |
English |
Contents |
Introduction
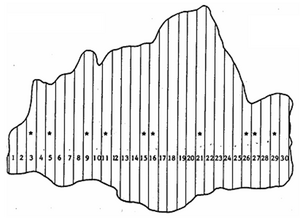
There are situations in forest inventory sampling in which the value of the target variable is known (or suspected) to be highly correlated to an other variable (called co-variable or ancillary variable). We know from the discussion on spatial autocorrelation and the optimization of cluster plot design that correlation between two variables means essentially that the one variable does yet contain a certain amount of information about the other variable. The higher the correlation the better can the value of the second variable be predicted when the value of the first is known (and vice versa). Therefore, if such a co-variable is there on the plot, it would make sense to also observe it and utilize the correlation to the target variable to eventually improve the precision of estimating the target variable. This is exactly the situation where the ratio estimator is applied.
A typical and basic example is that of sample plots of unequal size, as depicted, for example in Figure 1 where strips of different length constitute the population of samples. Another example would be clusters of unequal size: while cluster sampling only deals with the case of clusters of equal size, the ratio estimator allows to take into account the differently sized sample plots. Here, obviously, the size of the sample plots is the co-variable that needs to be determined for each sample plot. That a high positive correlation is to be expected between most forestry-relevant attributes and plot size should be obvious: the larger the plot the more basal area, number of stems, volume etc. is expected to be present.
References
| sorry: |
This section is still under construction! This article was last modified on 12/29/2010. If you have comments please use the Discussion page or contribute to the article! |
Cite error:
<ref> tags exist, but no <references/> tag was found