The trigonometric principle
| (53 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Ficontent}} {{video|link=https://youtu.be/XqupMoiafMY}} |
| − | The so-called trigonometric principle of | + | |
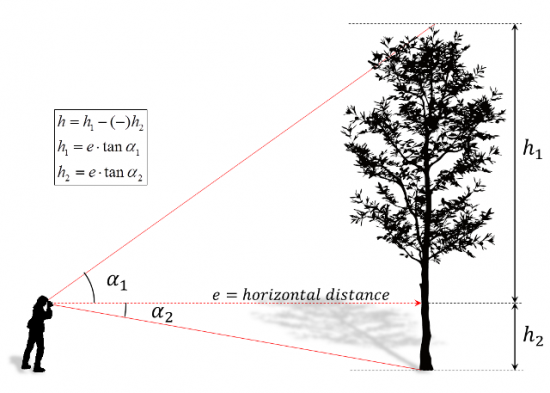
| + | The so-called trigonometric principle of [[tree height|height measurement]] bases on the measurement of angles as illustrated in the following figure. Height values per inclination angle are then calculated by | ||
| + | |||
| + | :<math>h=e*\tan \alpha \,</math> | ||
| + | |||
| + | if the inclination is measured in degrees or | ||
| + | |||
| + | :<math>h=e*\frac{p}{100} \,</math> | ||
| + | |||
| + | if inclination is measured in percent; <math>e</math> is the [[Distance to tree|horizontal distance]]. These basic formula allow calculating what is given as <math>h1</math> and <math>h2</math> in the figure. | ||
| + | |||
| + | [[file:tree_height_horizontal.png|550px|center]] | ||
| + | |||
| + | To calculate total [[tree height]], these two height values need to be added. However, in order to make this calculation more general and also applicable to all applications in [[Measuring slope|sloped terrain]], we say, that we subtract the two resulting height measurements, where it must be observed that in the case of the above figure the angle <math>{\alpha}2</math> is a negative angle producing a negative height value. | ||
| + | |||
| + | Therefore, as a general rule to calculate total tree height, we calculate the difference between upper measurement and lower measurement as | ||
| + | |||
| + | :<math>h=e*(\tan \alpha_1 - \tan \alpha_2) \,</math> | ||
| + | |||
| + | while always taking into account that angle measurements below the horizontal will produce negative height values. This general formula does also work for height measurements in sloped terrain where it does not make a difference whether we measure from above or from below the tree. | ||
| + | |||
| + | {{info | ||
| + | |message=Note: | ||
| + | |text=If you just remember to calculate <math>h_1-h_2</math> (while observing the sign of <math>h_2</math>!!) you are on the save side, no matter whether the observer stands above or below the stem base in sloped terrain! | ||
| + | }} | ||
| + | |||
| + | There are various [[:Category:Measurement devices|devices]] for measuring heights along the trigonometric principle, such as [[Haga]], [[Relascope|Spiegelrelaskop]] (relascope), the [[Suunto]] and [[Blume-Leiss]] height meters. Further most of the more modern instruments, like [[Vertex]] or other devices work based on the described principle. The scales of the instruments allow reading tree height directly whenever the indicated [[horizontal distance]] from the tree is kept; these distances are usually 15m or 20m (sometimes also 30m and 40m). Only for these fixed distances the tree heights can then be read directly from the instrument. Those modern instruments that include a rangefinder (laser or ultrasonic sound) a fixed distance is not necessary. | ||
| + | |||
| + | For all other distances we need to modify the value read from the instrument proportionally. That is, if we read a tree height <math>h</math> for the distance of 20m, but in fact we are 40 m away the true height measurement is <math>2h</math>. This is important as we do not always make it to find a place in the stand at exactly the prescribed distance to the [[Tree Definition|tree]]. In fact, the optimal distance to the tree for height measurements along the trigonometric principle is at about one to one and a half tree height. If we go closer, it will be more and more difficult to aim at the top of the tree (in particular for deciduous species), if we go farther away, the angle measurements become less and less accurate. | ||
| + | |||
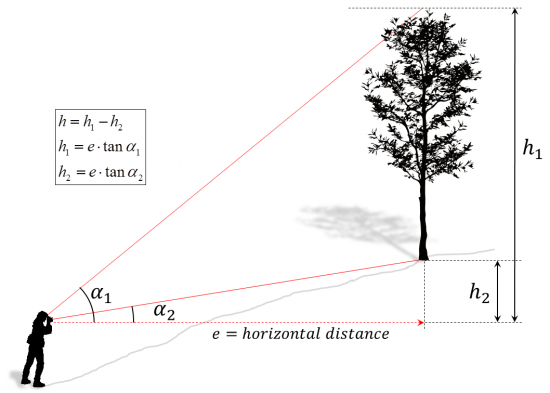
| + | ==Measuring tree heights in sloped terrain== | ||
| + | [[file:tree_height_slope.png|550px|center]] | ||
| + | |||
| + | {{info | ||
| + | |message=Note: | ||
| + | |text=If one uses a [[:Category:measurement devices|measurement device]] which does not enable to directly measure [[horizontal distance]]s (or e.g. rely on fixed distances to the tree determined by optical principles) the measured distance has to be corrected (or the resulting tree height). To avoid corrections in sloped terrain a practical solution is to move parallel to the slope and to find a position from which one can directly measure the horizontal distance. | ||
| + | }} | ||
| + | |||
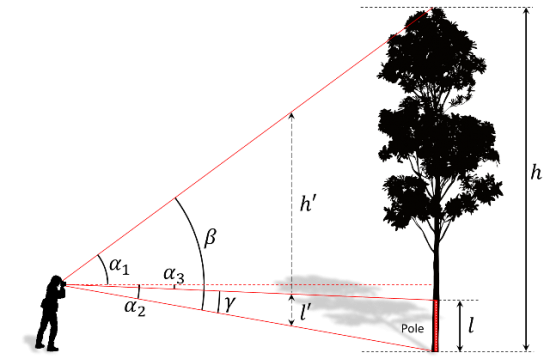
| + | ==Measuring height without given distance== | ||
| + | There may be situations in which the measurement of a distance is not possible. Then, a variation of the trigonometric principle can be applied: a pole of known length is put perpendicularly next to the tree and the viewer takes an additional angle measurement <math>{\alpha}3</math> to the top of this pole. | ||
| + | |||
| + | The tree height <math>h</math> is derived as usual from | ||
| + | |||
| + | :<math>h=e*(\tan \alpha_1 - \tan \alpha_2) \,</math> | ||
| + | |||
| + | and the length <math>l</math> of the pole derives from the same formula: | ||
| + | |||
| + | :<math>h=e*(\tan \alpha_3 - \tan \alpha_2) \,</math> | ||
| + | |||
| + | [[file:tree_height_pole.png|550px|center]] | ||
| + | |||
| + | As the length <math>l</math> of the pole is known, we can determine the horizontal distance <math>e</math> from | ||
| + | |||
| + | :<math>e=\frac{l}{(\tan \alpha_3 - \tan \alpha_2)} \,</math> | ||
| + | |||
| + | and inserting this into the tree height formula, what eventually yields: | ||
| + | |||
| + | :<math>h=\frac{(\tan \alpha_1 - \tan \alpha_2)}{(\tan \alpha_3 - \tan \alpha_2)} \,</math> | ||
| + | |||
| + | With this formula we calculate tree height along the trigonometric principle without having to measure the distance to the tree. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | {{SEO|keywords=trigonometric principle,tree height,forest inventory,tree measurement,single tree variables | ||
| + | sampling|descrip=The trigonometric principle of tree height measurement bases on the measurement of angles.}} | ||
| − | |||
[[Category:Tree height]] | [[Category:Tree height]] | ||
Latest revision as of 09:03, 12 March 2021
The so-called trigonometric principle of height measurement bases on the measurement of angles as illustrated in the following figure. Height values per inclination angle are then calculated by
\[h=e*\tan \alpha \,\]
if the inclination is measured in degrees or
\[h=e*\frac{p}{100} \,\]
if inclination is measured in percent; \(e\) is the horizontal distance. These basic formula allow calculating what is given as \(h1\) and \(h2\) in the figure.
To calculate total tree height, these two height values need to be added. However, in order to make this calculation more general and also applicable to all applications in sloped terrain, we say, that we subtract the two resulting height measurements, where it must be observed that in the case of the above figure the angle \({\alpha}2\) is a negative angle producing a negative height value.
Therefore, as a general rule to calculate total tree height, we calculate the difference between upper measurement and lower measurement as
\[h=e*(\tan \alpha_1 - \tan \alpha_2) \,\]
while always taking into account that angle measurements below the horizontal will produce negative height values. This general formula does also work for height measurements in sloped terrain where it does not make a difference whether we measure from above or from below the tree.
 Note:
Note:
- If you just remember to calculate \(h_1-h_2\) (while observing the sign of \(h_2\)!!) you are on the save side, no matter whether the observer stands above or below the stem base in sloped terrain!
There are various devices for measuring heights along the trigonometric principle, such as Haga, Spiegelrelaskop (relascope), the Suunto and Blume-Leiss height meters. Further most of the more modern instruments, like Vertex or other devices work based on the described principle. The scales of the instruments allow reading tree height directly whenever the indicated horizontal distance from the tree is kept; these distances are usually 15m or 20m (sometimes also 30m and 40m). Only for these fixed distances the tree heights can then be read directly from the instrument. Those modern instruments that include a rangefinder (laser or ultrasonic sound) a fixed distance is not necessary.
For all other distances we need to modify the value read from the instrument proportionally. That is, if we read a tree height \(h\) for the distance of 20m, but in fact we are 40 m away the true height measurement is \(2h\). This is important as we do not always make it to find a place in the stand at exactly the prescribed distance to the tree. In fact, the optimal distance to the tree for height measurements along the trigonometric principle is at about one to one and a half tree height. If we go closer, it will be more and more difficult to aim at the top of the tree (in particular for deciduous species), if we go farther away, the angle measurements become less and less accurate.
[edit] Measuring tree heights in sloped terrain
 Note:
Note:
- If one uses a measurement device which does not enable to directly measure horizontal distances (or e.g. rely on fixed distances to the tree determined by optical principles) the measured distance has to be corrected (or the resulting tree height). To avoid corrections in sloped terrain a practical solution is to move parallel to the slope and to find a position from which one can directly measure the horizontal distance.
[edit] Measuring height without given distance
There may be situations in which the measurement of a distance is not possible. Then, a variation of the trigonometric principle can be applied: a pole of known length is put perpendicularly next to the tree and the viewer takes an additional angle measurement \({\alpha}3\) to the top of this pole.
The tree height \(h\) is derived as usual from
\[h=e*(\tan \alpha_1 - \tan \alpha_2) \,\]
and the length \(l\) of the pole derives from the same formula:
\[h=e*(\tan \alpha_3 - \tan \alpha_2) \,\]
As the length \(l\) of the pole is known, we can determine the horizontal distance \(e\) from
\[e=\frac{l}{(\tan \alpha_3 - \tan \alpha_2)} \,\]
and inserting this into the tree height formula, what eventually yields:
\[h=\frac{(\tan \alpha_1 - \tan \alpha_2)}{(\tan \alpha_3 - \tan \alpha_2)} \,\]
With this formula we calculate tree height along the trigonometric principle without having to measure the distance to the tree.